Circuit AnalysisEE CalculatorsFormulas - EquationsHow To
Cramer’s Rule Calculator – 2 and 3 Equations System
Cramer’s Rule & Calculator for Linear Circuit Analysis | Step by Step with Solved Examples
Today, we are going to share another simple but powerful circuit analysis technique which is known as “Cramer’s Rule“.
Update: We have added Online Cramer’s Rule Calculator where you can solve two equations system as well as three equations system. Check both Cramer’s rule calculator in both sections of the post. Thanks
Below is the Step by Step tutorial of solved examples, which elaborates that how to solve a complex electric circuit and network by Cramer’s rule.
Cramer’s Rule Calculator for 2×2 (Two Equations System)
Example 2:
Use Mesh Analysis to determine the three mesh currents in the circuit below. Use Cramer’s rule for simplification.

First of all, apply the KVL on each mesh one by one, and write its equations.
-7+1(i1–i2) +6+2(i1–i3) = 0
1(i2– i1) + 2i2 + 3(i2– i3) = 0
2(i3– i1) – 6+3(i3– i2) +1i3 = 0
Simplifying,
3i1 – i2 – 2i3 = 1 … Eq….. (1)
– i1 + 6i2 – 3i3 = 0 … Eq….. (2)
-2i1 – 3i2 + 6i3 = 6 … Eq….. (3)
Now, write the above equations in the matrix form.
3i1– i2– 2i3 = 1
–i1+ 6i2– 3i3 = 0
-2i1– 3i2+ 6i3 = 6

Now, we will find the coefficient determinant of ∆. How will we do that? Just check the fig below for better explanation.
So the full step is shown below.

∆ = +3 (6 x 6) – (- 3 x –3) – (-1 (-1 x 6)-(-2 x –3) + (-2 (-1 x –3) – (-2 x 6)
∆ = 81 -12 -30 = 39
Now, find the ∆1 by the same way as explained above. But, just replace the first column of the matrix with the “Answer Column”. For detail, check the fig shown below.
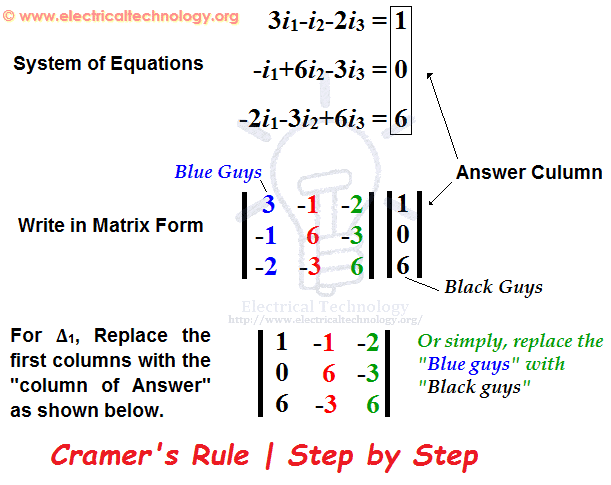
So, here is the full step to find ∆1. Here, we replaced the “Blue Guys” in the first column with “Black Guys” :).

= +1(36-9) – (–1[0+18]) –2(0-36)
= 27 + 18 + 72
∆1 = 117
Again, find the ∆2 with the same method as explained earlier. Just replace the second column of the matrix with the “Answer column” i.e. replace the “Red guys” in the center column with “Black Guys” as shown below.
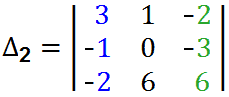
= +3 (0 +18) -1[(-6)-(+6)] –2(-6-0)
= 54+12+12 = 78
∆2 = 78
Finally, find the last ∆3. Just replace the third column with the “Answer column” i.e. replace the “Green guys in the third column with “Black guys” as shown below.

= +3 (6 x 6) – (-3 x 0) – [-1(-1 x 6) – (-2 x 0)] + [1(-1) x (-3) – (-2) x (6)]
= 108 + 6 + 15
∆3 = 117
Now, solve and find the unknown values of current, i.e. i1, i2 and i3.
As, Cramer’s rule says that, variables i.e. i1 = ∆1/∆1, i2 = ∆/∆2 and i3 = ∆/∆3.
Therefore,
i1 = ∆1/∆1
= 117/39
i1 = 3A
And i2,
i2 = = ∆/∆2
= 78/39
i2 = 2A
And finally, i3;
i3 = ∆/∆3
= 117/39
i3 = 3A.
I hope that you understood the cramer’s rule very well and enjoyed the step by step tutorial. Please, don’t forget to share with your friends. Also, enter your email address in the below box to subscribe. So, we will send you more tutorials like the above one. Thanks.
Related Posts and Circuit Analysis Tools:
- Norton’s Theorem. Easy Step by Step Procedure with Example (Pictorial Views)
- Thevenin’s Theorem. Easy Step by Step Procedure with Example (Pictorial Views)
- Electrical & Electronics Engineering Calculators Online
- 10+ Design & Simulation Tools for Electrical/Electronics Engineers Online
- PCB Designing: How To Design a PCB (Step by Step & Pictorial Views)
- 15 Must Have Android Apps for Electrical & Electronics Engineers & Students
- SUPERNODE Circuit Analysis | Step by Step with Solved Example
- SUPERMESH Circuit Analysis | Step by Step with Solved Example
- Electrical and Electronics Eng Calculators









it is very nice i like so macth
How to find linear equation which is represent in form AX=B
where Matrix A in 4×2 Matrix(any Matrix).no other detail of B given
Nice and good
Very nice.. thanks alot