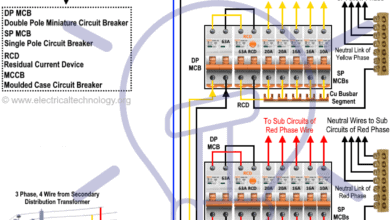
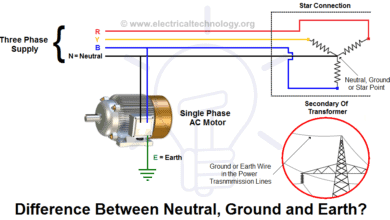
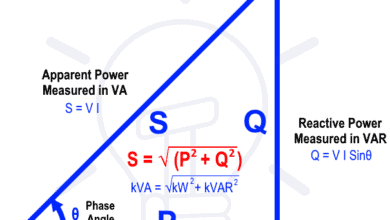
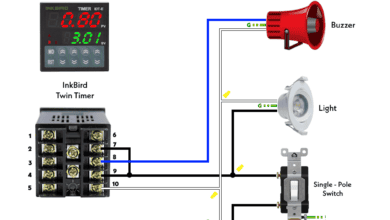
1-Phase Circuits
Components of Admittance. ( Simple Explanation)
Components of Admittance.
Conductance:
A component of admittance inphase with the applied voltage is called conductance. Or the X component of admittance is called conductance. It’s represented by G and the unit of conductance is Mho or Siemens.
G = Y Cos φ = (1/Z) * (R/Z) = R/Z2 = R/ (R2 + X2)
(Since Cos φ = R/Z and Y = 1/Z)
And Total Conductance GT = G1 +G2 +G3+…..
Susceptance:
That component of admittance, which has an angle of 90 degree with applied voltage is called suserptance. ..or Y component of admittance is celled susceptnce, its represented by B. and the unit of susceptance is also Mho or Siemens.
OR
A Component of admittance in quadrature ( at 90 degree) with the applied Voltage is called susceptance.
B = Y Sin Φ = 1/Z * X/Z = X/Z2 = X/ (R2 + X2) ——–> (Since Sine Φ = X/Z)
And total Susceptance = BT = B1 + B2 + B3 +…Bn
Also Note that inductive suseptance of a circuit is negative (-), while Capacitive Susceptance of a circuit is always positive (+).
Y = G – j BL …… (In case of inductive Circuit)
Y = G + BC ……. (In case of capacitive circuit)
For More explanation, consider the following circuit, (fig 1)
The Total conductance = algebraic sum of the conductance in each branch.
The Total conductance =GT= G1 +G2 +G3
Similarly,
Total susceptance = algebraic sum of the susceptance in each branch,
Total susceptance BT = (-B1) + (-B2) + (B3).
And total circuit admittance,
YT = √ (GT2 + BT2)
In case of inductive Circuit YT = √ (G2 + BL2) and Phase angle φ tan-1 (-BL/G)
In Case of Capacitive Circuit YT = √ (G2 + BL2) and phase angle φ tan-1 (Bc /G)
And Total current, I = VY,