Exclusive-OR (XOR) Digital Logic Gate
Exclusive-OR Gate – Digital Logic XOR Gate
What is Logic XOR or Exclusive-OR Gate?
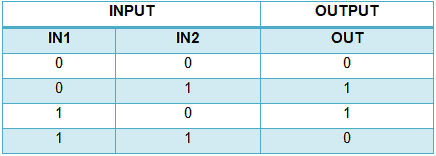
XOR gate also known as Exclusive OR gate is “A logic gate which produces HIGH state ‘1’ only when there is an odd number of HIGH state ‘1’ inputs”.
For 2-input gate it can be interpreted as “when both of the inputs are different, then the output is HIGH state ‘1’ and when the inputs are same, then the output is LOW state ‘0’”.
XOR gate can have two or more than two inputs but it has only one output.
XOR Gate Logic Symbol, Boolean Expression & Truth Table
XOR Gate Symbol
There are 3 types of symbols used for XOR gate all over the world.
American National Standards Institute (ANSI)/ MILITARY
International Electrotechnical Commission (IEC)/EUROPEAN
Deutsches Institut für Normung (DIN)/GERMANY
Boolean Expression
OUT = ( I̅N̅1 & IN2) + (IN1 & I̅N̅2) or OUT = (I̅N̅1 + I̅N̅2) & (IN1 + IN2) ;
Truth Table
XOR Gate Logic flow Schematic Diagram
Construction and Working Mechanism of XOR Gate
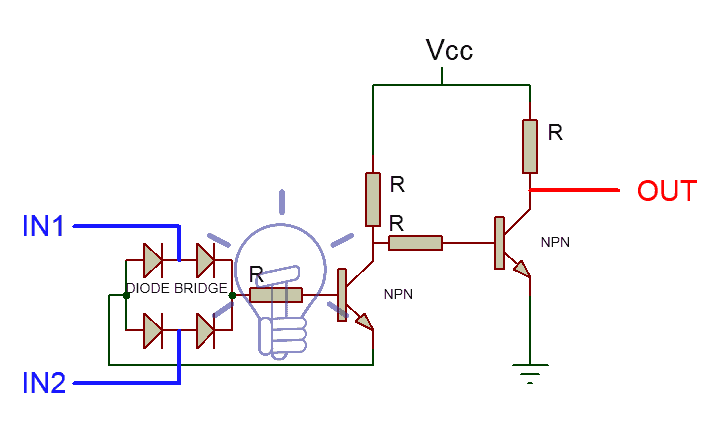
XOR Gate Using BJT and Diodes
Schematic of XOR gate using Diodes and BJT (NPN transistor) is given below. In which we have used two NPN transistors, 4 diodes and the resistor between Diode Bridge and NPN is used in series configuration because BJTs operates on input current, not input voltages.
The diodes are used in a bridge configuration (Rectifier) to sort out the input logic into the positive level, means if there is a High state input it will always flow to the base of NPN to switch it on. And the Low state will always flow out to the emitter of NPN transistor.
The first transistor is used for switching upon the input logic given to it. And the second NPN transistor is nothing more than just an Inverter. It only inverts the output of the first NPN transistor.
When inputs are different, the high state flow to NPN transistor’s base and turn it ON. The LOW state “0” flow through the emitter to the base of the 2nd NPN transistor and inverts into Logic HIGH state “1” as output.
When the inputs are same, if it’s LOW state “0” then NPN will never turn on because there be no HIGH state input at its base. So Vcc will flow out to the inverter phase and it will invert into Low state “0” as output. If it’s HIGH state “1” then the NPN will turn on but there will be no Logic 0 to flow through the emitter. So again Vcc will flow through an inverter and invert into low state”0” as output.
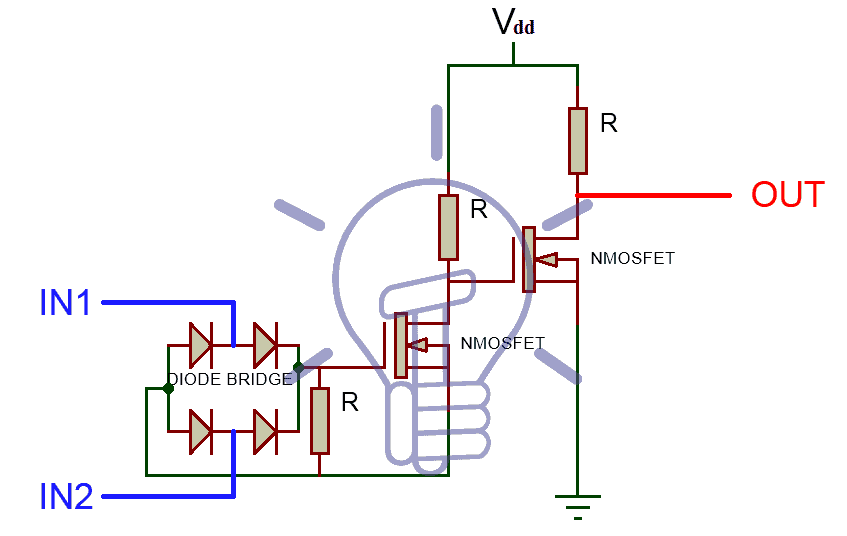
XOR Gate Using MOSFET and Diodes
Discrete XOR gate can be made with MOSFETs and diodes. XOR schematic using N-MOSFETs and diodes is given below.
In this schematic 4 diodes are used in a bridge configuration for sorting out input logic. 2 NMOSFETs are used; 1st one for switching upon input logic and the 2nd one for Inverting output of 1st NMOSFET. The resistor between Diode Bridge and 1st MOSFET is used in parallel configuration because MOSFETs operates on Gate’s voltages, not current.
When both inputs are different, then the High state will flow to NMOSFET’s gate and the LOW state will flow to NMOSFET’s source to build up potential at its gate, which will switch it ON. And the LOW state will flow out to the inverter and inverts into HIGH state “1”.
When both of the inputs are same i.e. if both are HIGH state “1” than the HIGH state will flow to the gate of NMOSFET but there will be no potential at its source so NMOSFET will switch OFF. Hence Vdd (HIGH state “1”) will flow to the inverter and inverts into LOW state “0” as output. When both inputs are LOW state “0”, again there will be no potential (voltage) at the gate of NMOSFET so it will never turn ON and Vdd will flow out to the inverter and inverts into LOW state “0” as output.
XOR Gate From other Logic Gates: (Combinational Logic)
XOR operation can be achieved with a combination of different logic gates.
Boolean expression of XOR is given below.
Sum of Product
In this expression, we use the sum of Min terms. Min terms are the product of inputs for which output is HIGH state “1”.
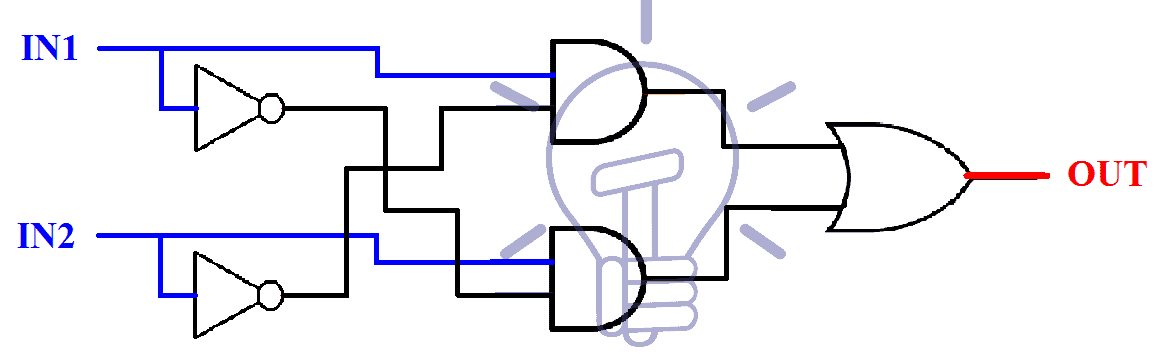
SOP expression can be easily implemented with NAND gates.
According to the truth table given above the SOP (sum of product) expression is:
OUT = (I̅N̅1 & IN2) + (IN1 & I̅N̅2)
This expression can be implemented with NOT, AND, OR gates as shown in the figure given below.
Product of Sum
In this expression, we use the product of Max terms. Max terms are the sum of inputs for which output is LOW state “0”.
POS expression can be easily implemented with NOR gates.
According to the truth table given above the POS (product of sum) expression is :
OUT = (I̅N̅1̅+I̅N̅2̅) & (IN1+IN2) Expression 1
OUT = (IN1 & IN2)’ & (IN1+IN2) Expression 2 DE MORGAN’S LAW
Expression 1 can be implemented with NOT, AND, OR gates as shown in the figure given below.
Expression 2 uses NAND, AND & OR gate to reduce the number of used gates as shown in the figure given below.
XOR Gate From Universal Gates
Universal gates are those gates which can be implemented into any logic gate or logic function.
XOR Gate From NAND Gate
NAND gate is a universal gate. It can be implemented into any Logic function.
As we have discussed before SOP (sum of product) expression can be easily Implemented with NAND gates, so SOP expression for XOR gate is
OUT = { (I̅N̅1 & IN2) + (IN1 & I̅N̅2) }
OUT’ = { (I̅N̅1 & IN2) + (IN1 & I̅N̅2) }’ Taking complement on both sides
OUT’ = { (I̅N̅1 & IN2)’ & (IN1 & I̅N̅2)’ } De Morgan’s Law
OUT’’ = { (I̅N̅1 & IN2)’ & (IN1 & I̅N̅2)’ }’ Taking complement on both sides
OUT = [ { (IN1 & IN1)’ & IN2}’ & { IN1 & (IN2 & IN2) }’ ]’ (IN1 & IN1)’ = I̅N̅1
Now, this expression is in NAND form. And can easily be implemented with NAND gates as shown in the figure below.
XOR Gate From NOR GATE
NOR gate is also a universal gate. It can be implemented into any Logic function.
As we have discussed before POS (product of sum) expression can be easily implemented with NOR gates, so POS expression for XOR gate is given below
OUT = { (I̅N̅1̅ + I̅N̅2̅) & (IN1 + IN2) }
OUT’ = { (I̅N̅1̅ + I̅N̅2̅) & (IN1 + IN2) }’ Taking complement on both sides
OUT’ = { (I̅N̅1̅ + I̅N̅2̅)’ + (IN1 + IN2)’ } De Morgan’s Law
OUT’’ = { (I̅N̅1̅ + I̅N̅2̅)’ + (IN1 + IN2)’ }’ Taking complement on both sides
OUT = [ { (IN1 + IN1)’ +(IN2 + IN2)’ }’ + (IN1 + IN2)’]’ (IN1 + IN1)’ = I̅N̅1
Now, this expression is in NOR form. And can easily be implemented with NOR gates as shown in the figure below.
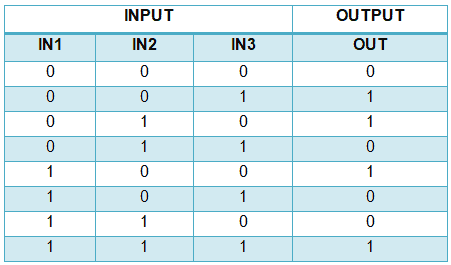
Multi-Input Exclusive OR Gate
XOR gate gives HIGH state “1” only when there is an odd number of HIGH state “1” inputs.
XOR gate can have more than two inputs but it has only one output.
Truth Table
The truth table of “3” inputs XOR gate is given below.
Construction:
Combinational Logic
Combinational logic is the logic of making a schematic with the help of basic logic gates.
Sum of products (SOP) and products of the sum (POS) are two methods in combinational logic.
Sum of Products
SOP uses the idea of summation of minterms (product of inputs for which output is high)
According to the truth table given above, Sum of product expression and schematic for 3-input XOR gate is given below.
OUT = (I̅N̅1̅ & I̅N̅2̅ & IN3) + (IN1 & I̅N̅2̅ & I̅N̅3̅) + (I̅N̅1̅ & IN2 & I̅N̅3̅) + (IN1 & IN2 & IN3)
Product of Sum
POS uses the idea of the product of max terms (Sum of inputs for which output is LOW.)
According to the truth table given above, Product of sum expression and schematic for 3-input XOR gate is given below.
OUT = (I̅N̅1 + IN2 + IN3) & (IN1 + I̅N̅2 + IN3) & (IN1 + IN2 + I̅N̅3) & (I̅N̅1 + I̅N̅2 + I̅N̅3̅)
TTL and CMOS Logic XOR Gate IC’s
Some of XOR IC with pin configurations is given below.
TTL Logic XOR Gate
- 74136 Quad 2-input (with open collector outputs)
- 7486 Quad 2-input
CMOS Logic XOR Gate
- 4070 Quad 2-Input
Pinout for 7486 TTL XOR Gate IC
| PIN Number | Description |
| 1 | Input Gate 1 |
| 2 | Input Gate 1 |
| 3 | Output Gate 1 |
| 4 | Input Gate 2 |
| 5 | Input Gate 2 |
| 6 | Output Gate 2 |
| 7 | Ground |
| 8 | Output Gate 3 |
| 9 | Input Gate 3 |
| 10 | Input Gate 3 |
| 11 | Output Gate 4 |
| 12 | Input Gate 4 |
| 13 | Input Gate 4 |
| 14 | Positive Supply Voltage |
Exclusive OR Gate Applications
Some common application and uses of XOR or Exclusive-OR gate are as follow:
- XOR is used as a comparator to know if the input signals are equal or not.
- XOR Gate is the crucial part of a Half Adder. it can produce the sum of two single bit numbers. Half Adder is the building block of the ALU (Arithmetic Logic Unit) which is used in every digital system.
- It can be used as parity checker to check if the data stream received is corrupted or not.
You may also read more about Digital logic gates.
Logic NOT Gate – Digital Inverter Logic Gate Digital Logic OR Gate Digital Logic AND Gate Digital Logic NOR Gate