Introduction to Signals, Types, Properties, Operation & Application
What is Signal, Classification of Signals and the Role of Signals in Digital Communication
What Is Signal?
A signal is defined as any physical or virtual quantity that varies with time or space or any other independent variable or variables.
Graphically, the independent variable is represented by horizontal axis or x-axis. And the dependent variable is represented by vertical axis or y-axis.
Mathematically, a signal is a function of one or more than one independent variables.
Single Variable Signal
It depends on a single independent variable. It either varies linearly or non-linearly depending on the expression of the signal. Examples of single variable signal are:
S(x) = x+5
S(x) = x2+5 Where x is the variable
S(t) = cos(wt+ϴ) Where t is the variable
Two Variables Signal
A two-variable signal varies with the change in the two independent variables. Example of a two-variable signal is
S(x,y) = 2x+ 5y
Characteristics Of Signal
A signal is defined by its characteristics. It shows the nature of the signal. These characteristics are given below:
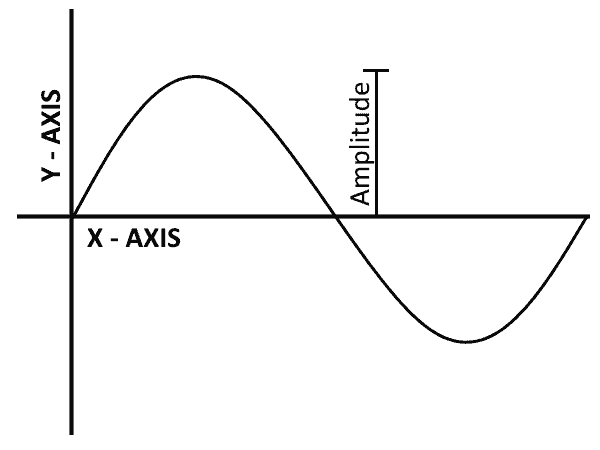
Amplitude
Amplitude is the strength or height of the signal waveform. Visually, it is the height of the waveform from its centerline or x-axis. The y-axis of a signal’s waveform shows the amplitude of a signal. The amplitude of a signal varies with time.
For example, the amplitude of a sine wave is the maximum height of the waveform on Y-axis.
The signal’s strength is usually measured in decibels db.
Frequency
Frequency is the rate of repetitions of a signal’s waveform in a second.
Periodic signals repeat its cycle after some time. The number of cycles in a second is known as Frequency. The unit of Frequency is hertz (Hz) and one hertz is equal to one cycle per second. It is measured along the x-axis of the waveform.
For example, a sine wave of 5 hertz will complete its 5 cycles in a one second.
Time Period
The time period of a signal is the time in which it completes its one full cycle. The unit of the time period is Second. The time period is denoted by ‘T’ and it is the inverse of frequency. I.e.
T=1/F
For example, a sine wave of time period 10 sec will complete its one full cycle in 10 seconds.
Phase
The phase of a sinusoidal signal is the shift or offset in its origin or starting point. The phase shift can be lagging or leading. Usually, the original sinusoidal signals have 0° degree phase and start at 0 amplitude but an offset in phase will shift its starting amplitude to other than 0.
An example of 45° phase shift is given below. The signal remains the same but its origin is shifted to 45°.
The phase shift can be from 0° to 360° in degrees or 0 to 2π in radians. 360° degree or 2π radians is one complete period.
Related Post: What is GSM and How does it Work?
Signal Size
The size of a signal is a number that shows the strength or largeness of that signal. As we know, a signal’s amplitude varies with respect to time. Because of this variation, we cannot say that its amplitude can be its size. To measure the signal size, we have to take into account the area covered by the amplitude of the signal within the time duration.
According to the size of the signal, there are two parameters.
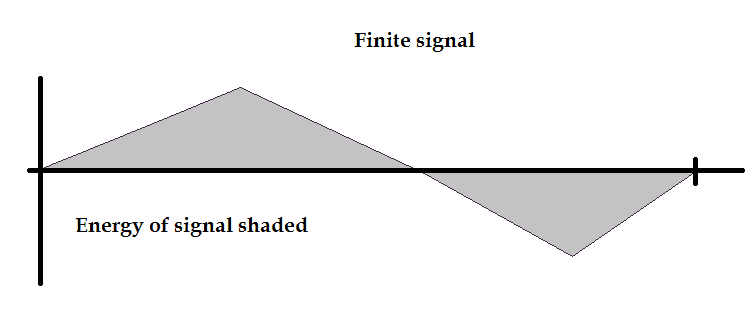
Signal Energy
The energy of the signal is the area of the signal under its curve. But the signal can be in both positive and negative region. Due to which, it will cancel each other’s effect resulting in a smaller signal. To eradicate this problem, we take the square of the signal’s amplitude which is always positive.
For a signal g(t), the area under the g2(t) is known as the Energy of the signal.
Unit Of Energy Of Signal
This energy is not taken as in its conventional sense, but it shows the signal size. Therefore, its unit is not joule. The unit of energy depends on the signal. If it is a voltage signal then its unit will be volts2/second.
Limitation
The energy of a signal can be measured only if the signal is finite. The infinite signal will have infinite energy, which is absurd. A finite signal’s amplitude goes to 0 as the time (t) approaches to infinity (∞).
So it is necessary that the signal is a finite signal if you want to measure its energy.
Signal Power
If the signal is an infinite signal i.e. its amplitude does not go to 0 as time t approaches to ∞, we cannot measure its energy. In such a case, we take the time average (Time period) of the energy of the signal as the power of the signal.
Unit Of Power
Similar to Energy of the signal, this power is also not taken in the conventional sense. It will also depend on the signal to be measured. If the signal is a voltage signal, then the power will be in volts2.
Limitation
Just like the energy of the signal, the measurement of the power of a signal also has some limitation that the signal must be of a periodic nature. An infinite and non-periodic signal neither have energy nor power.
Classification Of Signals
Signals are classified into different categories based on their characteristics. Some of these categories are given below.
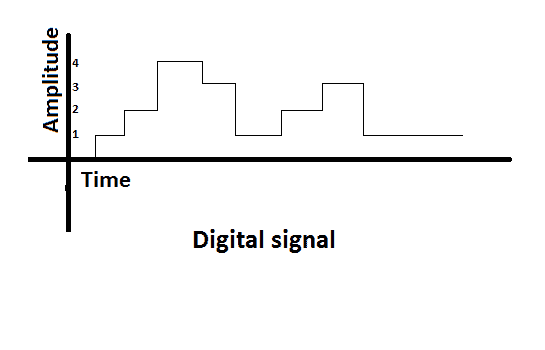
Analog Vs. Digital Signal
The signal can be classified into analog or digital category base on their amplitude. This classification is based on only vertical-axis (amplitude) of the signal. And it does not have any relation with horizontal-axis (time axis).
The amplitude of an analog signal can have any value (including fractions) at any point in time. That means analog signal have infinite values.
However, the digital signal’s amplitude can only have finite and discrete values.
The special case of Digital signal having two discrete values is known as Binary signal. However, the number of values for amplitude in a digital signal is not limited to only two.
Analog signal is converted into Digital signal using A to D converter (ADC).
- Related Post: What are Industrial Communication Networks? An Overview
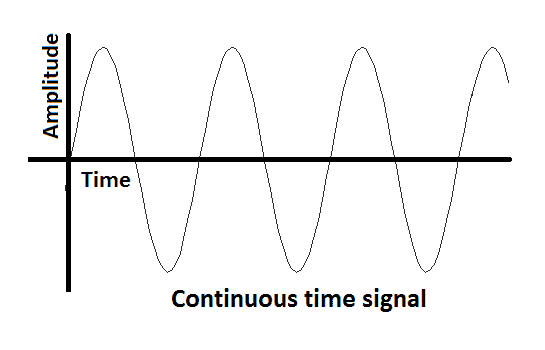
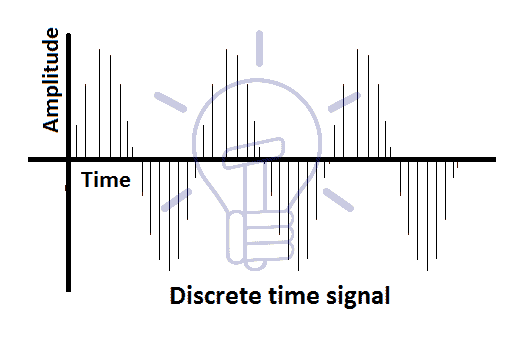
Continuous-Time And Discrete-Time Signal
This classification is based on the horizontal axis (time axis) of the signal.
Continuous and discrete time signals should not be confused with analog and digital signal respectively.
A continuous time signal is a signal whose value (amplitude) exists for every fraction of time t.
A discrete time signal exists only for a discrete value of time t.
Remember, there is no limitation on the amplitude of the signal. That is why it should not be confused with the analog or digital signal.
Energy Vs. Power Signal
A signal is Energy signal if its amplitude goes to 0 as time approaches ∞. Energy signals have finite energy.
Similarly, a signal with finite power is known as Power signal. A power signal is a periodic signal i.e. it has a time period.
An Energy signal has finite Energy but zero power. And a Power signal has finite Power but infinite Energy. So a signal can be either energy signal or power signal but it cannot be both.
An infinite signal that has no periodic nature is neither Energy nor Power signal.
Periodic Vs. Aperiodic Signal
A periodic signal is a signal which keeps repeating its pattern after a minimum fixed time. That time is known as Time period ‘T’ of that signal. The periodic signal does not change if it is time-shifted by any multiple of the Time period “T”.
The mathematical expression for periodic signal g(t) is:
T0 is the Time period of signal g(t).
The periodic signal starts from t=-∞ and continues to t=+∞. A signal which starts at t=0 will not be the same signal if it is time-shifted by +T because it did not exist for negative t.
The aperiodic or non-periodic signal is a signal which does not repeat itself after a specific time. These signals have no repetitions of any pattern.
Deterministic And Random Signal
A signal which can be represented in mathematical or graphical form is called deterministic signal. Deterministic signals have specified amplitude, frequency etc. They are easy to process as they are defined over a long period of time and we can Evaluate its outcome if they are applied to a specific system based on its expression.
The random or non-deterministic signal is a signal which can only be represented in probabilistic expression rather than its full mathematical expression. Every signal that has some kind of uncertainty is a random signal. Noise signal is the best example of the random signal.
Generally, every message signal is a random signal because we are uncertain of the information to be conveyed to the other side.
Operation Of Signal
Some basic operation of signals are given below
Time Shifting
Time-shifting means movement of the signal across the time axis (horizontal axis). A time shift in a signal does not change the signal itself but only shifts the origin of the signal from its original point along time-axis.
Basically, addition in time is time shifting. To time-shift a signal g(t), t should be replaced with (t-T), where T is the seconds of time-shift. Therefore, g(t-T) is the time-shifted signal by T seconds.
Time shift can be right-shift (delay) or left-shift (advance).
If the time-shift T is positive than the signal will shift to the right (delay). For example, the signal g(t-4) is the shifted version of g(t) with 4 seconds delay.
If the time-shift T is negative than the signal will shift to the left (advance). The signal g(t+4) is the shifted version of g(t) with 4 seconds to the left.
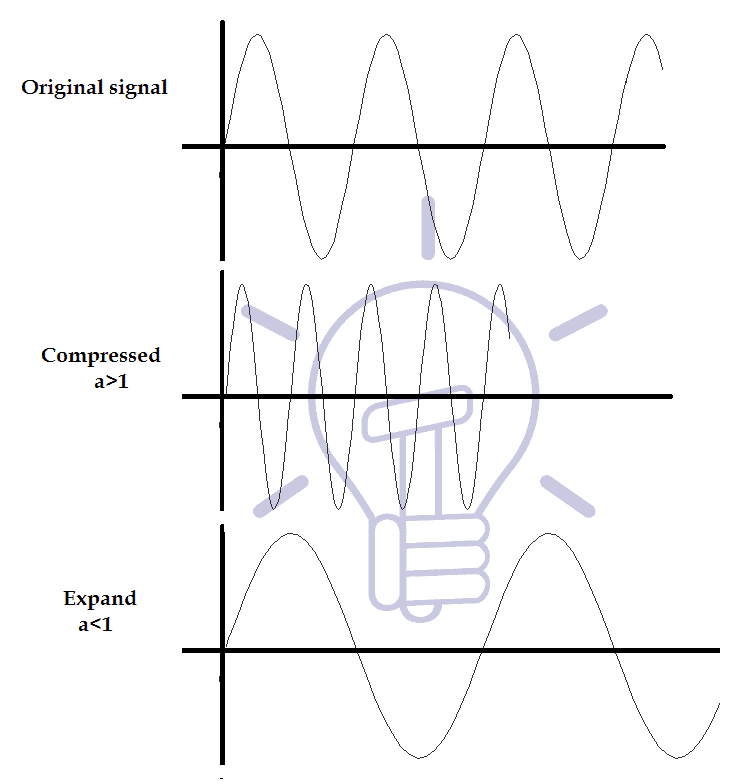
Time Scaling
Time scaling of a signal means to compress or expand the signal. It is achieved by multiplying the time variable of the signal by a factor. The signal expands or compresses depending on the factor.
Suppose a signal g(t) than its scaled version is g(at).
If the factor a>1 then the signal will compress. And the operation is called signal compression. Compressing a signal will make the signal fast as it becomes smaller and its time duration become less.
If a<1 then the signal will expand. And the operation is called signal dilation.
After scaling, the origin of the signal remains unchanged. Expanding the signal will make the signal slow as it becomes wider and covers more time duration.
Time Inversion
In time inversion, the signal is flipped about the y-axis (vertical axis). The resultant signal is the mirror image of the original signal.
Time inversion is a special case of time-scaling in which the factor a=-1. Therefore to invert a signal, we replace it’s (t) with (-t).
Mathematically, the time-invert of signal g(t) is g(-t).
Related Posts
- Types of Control & Communication Cables
- What is Industrial Automation | Types of Industrial Automation
- Why Radio Waves Are Chosen For Close Range Transmission?
- Serial Communication by Arduino





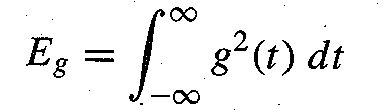












very simple and excellent way of explanation.Great.