RMS Voltage Calculator – From Average Value, Peak & Peak to Peak Value
RMS Voltage Value Calculator
This calculator can be used to calculate the RMS Voltage value (VRMS) of a sine wave from different related values such as average value (VAV), peak or max value (VP or VMAX) and peak to peak value (VP-P).
- Related Post: Peak Voltage and Peak to Peak Voltage Calculator
How to Calculate RMS Voltage Value ?
As discussed before about the Root Mean Square (RMS) or VRMS voltage, It is DC equivalent voltage of a sine wave i.e. if the RMS voltage value is 230VAC generating 60W heat when connected across an heating element such as resistor, the same amount of heat can be generated via DC voltage source of 230VDC when connected to the same heating element as connected before in AC Circuit.
We will show different equations for R.M.S Voltage calculation with applied formulas and solved examples as follow.
Related Calculator: 3, 4, 5 and 6 band Resistors Value Calculator
Equations for RMS Value Calculator
As the RMS voltage calculator is related to average value (VAV), peak or max value (VP or VMAX) and peak to peak value (VP-P), the following related equations for RMS Voltage calculator are shown in fig 2.
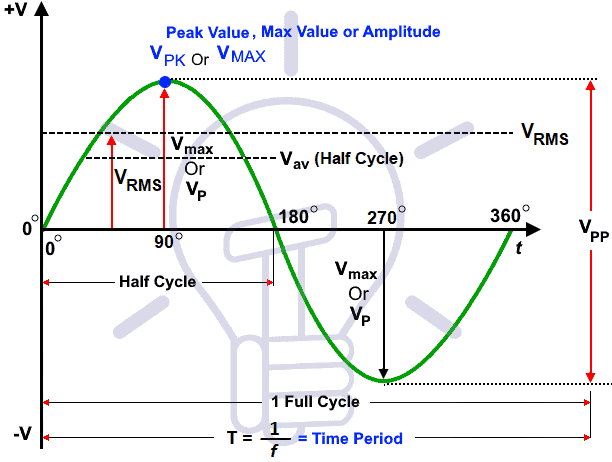
Peak Value: VP or VMAX
The maximum value, positive or negative, of an alternating quantity (such as voltage or current) is known as its amplitude of the waveform, max value or peak value. Its denoted by VP, IP or EMAX and IMAX.
VP = √2 x VRMS
By using the above formula, we may find the value of RMS voltage value as follow:
VRMS = 0.7071 x VP
Example:
Suppose the Peak Voltage value is 325VAC, the value of RMS Voltage will be:
VRMS = 0.7071 x 325V = 229.80 VRMS
-
Related Post: Peak Voltage and Peak to Peak Voltage Calculator
Peak to Peak Value (VPP)
The sum of positive and negative peak values in a sine wave is known as peak to peak value. Its expressed as IPP or VPP.
VPP = 2√2 x VRMS
By using the above formula, we may find the value of RMS voltage value as follow:
VRMS = 0.35355 x VPP
Example:
Suppose the Peak-Peak Voltage value is 340VAC, the value of RMS Voltage will be:
VRMS = 0.35355 x 340V = 120.2 VRMS
Related Calculators:
- Electrical Wire & Cable Size Calculator (Copper & Aluminum)
- Advance Voltage Drop Calculator and Voltage Drop Formula
Average Voltage Value (VAV)
If we convert the alternating current (AC) sine wave into direct current (DC) wave through rectifiers, then the converted value to the DC is known as the average value of that alternating current sine wave.
Keep in mind that the average voltage value of full AC sine wave is zero because the area covered by poitive half cycles is equal to the area covered by the negative half cycle which cancel each other. That’s why we can’t use AC to store in batteries.
We only use half wave to measure the average value of voltage or current in AC.
VAV = (2√2) / π x VRMS
By using the above formula, we may find the value of RMS voltage value as follow:
VRMS = 1.11 x VAV
Example:
Suppose the average Voltage value is 200VAC, the value of RMS Voltage will be:
VRMS = 1.11 x 200V = 222 VRMS
Related Post:
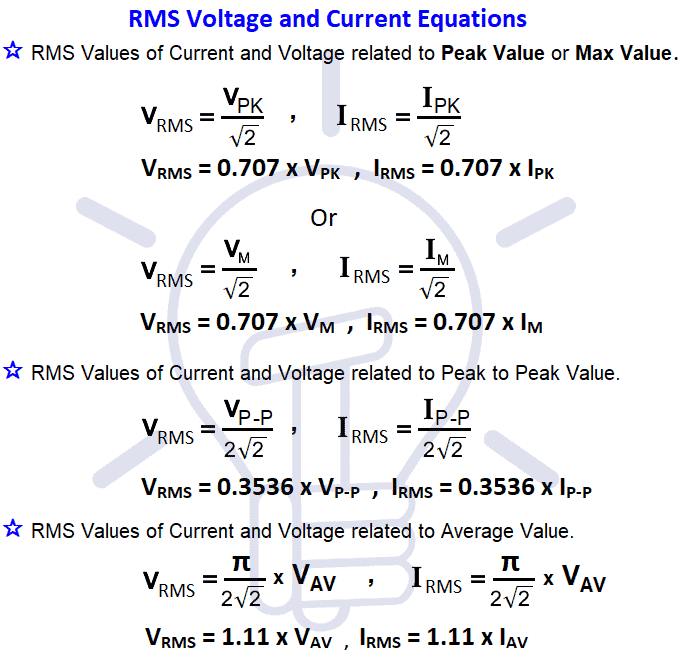





Your explanation is very helpful for electrical people.Thanks
I always find interest in Electrical Engineering matters. Your explanations are very useful. Thanks.