Comparator and Digital Magnitude Comparator
Digital Comparator and Magnitude Comparator
What is Digital Comparator?
Digital comparator is a device that used in combinational logic systems for comparing two binary numbers. It takes binary numbers as inputs and produces 3 outputs; whether the numbers are greater than, less than or equal to each other. They are made of AND, NOT & NOR Gates.
Digital Magnitude Comparator
Digital Magnitude Comparators are used in micro controller and CPUs for address comparing of data and register and other arithmetic operations. It has variety of uses in the digital world. Every auto-turn-off device uses a comparator.
The comparator is a decision-making device and it can be implemented in various control devices.
Comparator IC has 2 inputs and 3 outputs. These 3 outputs are connected with separate operations. These 3 operations are briefly discussed below.
- You may also read: Ring Counter & Johnson Counter – Construction & Operation
Basic Operation Terms of Comparator
Consider two binary numbers “A” and “B” as inputs to the digital comparator
- LESS THAN:
- If binary number “A” is less than “B” than “less than” output will produce HIGH state “1” also known as true.
- If binary number “A” is greater than or equal to “B” than “less than” output will produce LOW state “0” also known as false.
- EQUAL TO:
- If and only if number A is equal to number B than “equal to” output will produce logic HIGH state “1”. Otherwise, the output will be LOW state “0”.
- GREATER THAN:
- If number A is greater than B than “greater than” output will produce HIGH state”1”.
- If A is less than or equal to B than “greater than” output will produce LOW state “0”.
- You may also read: Digital Flip-Flops – SR, D, JK and T Flip Flops
Single Bit Comparator
This is the basic unit of a multi bit comparator which compares a single binary bit and produces output according to those bits.
We will briefly discuss its 3 Operation one by one with schematics and expressions.
Consider A,B be the inputs bits
Less than
The output of “less than” is represented by (A< B)
According to the truth table of Single Bit Comparator Sum of Product expression for A<B is
(A<B) = A̅B
Which can be implemented as:
Its output will be only true when “A” is less than “B”.
Equal to
The output of “Equal to ” is represented by (A = B)
According to the truth table of Single Bit Comparator Sum of Product expression for A=B is
(A=B) = A̅B̅ + AB
Which can be implemented as:
Observe the expression above. You will notice that XNOR expression is exactly the same. So it can also be replaced with XNOR as shown in below figure
We will represent it with ‘X’ such that
X = A̅B̅ + AB = (A XNOR B)
It will be only true when both A and B bits are same.
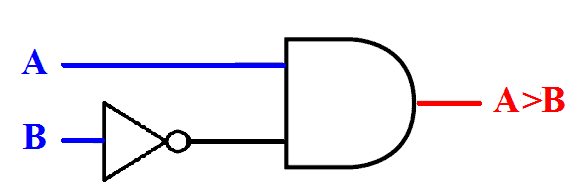
Greater than
The output of “less than” is represented by (A>B)
According to the truth table of Single Bit Comparator Sum of Product expression for A>B is
(A>B) = AB̅
Which can be implemented as:
Its output will be only true when “A” is greater than “B”.
- You may also read: Ripple Carry And Carry Look Ahead Adder
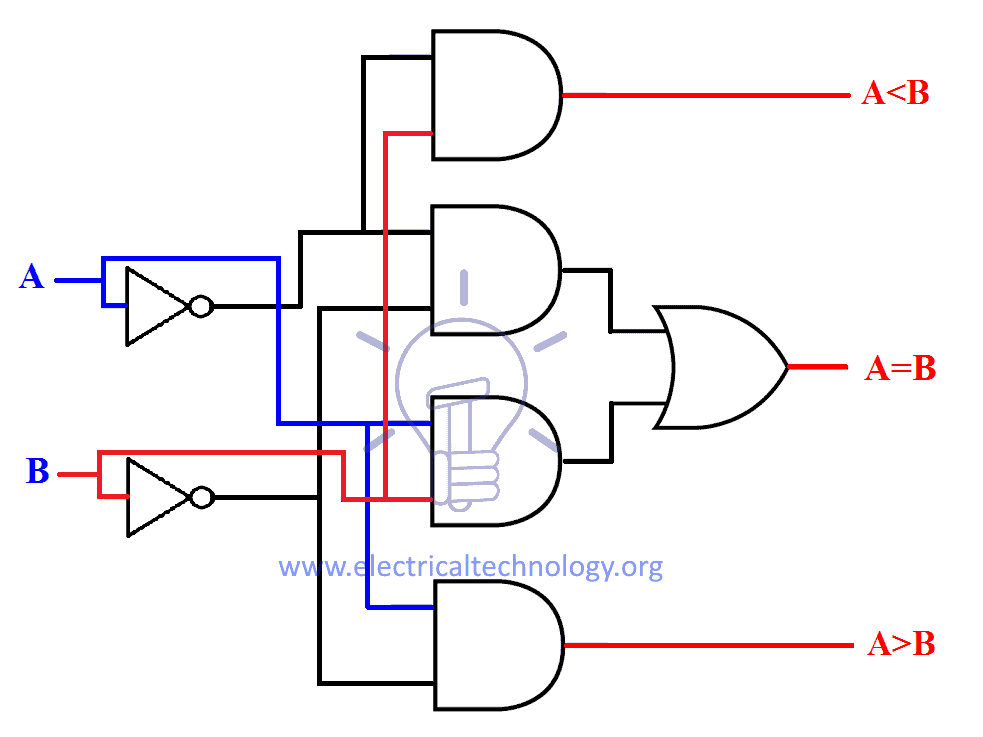
Full Comparator
Now we will combine all these three operations into a single schematic. which will form a single bit comparator as given below.
Comparator Without XNOR
Comparator Using XNOR
“n” Bits Comparator
The comparator which can compare “n” bit size of the number. ‘n’ can be any positive digit. It can be made from single bit comparator,
When you understand “n” bit comparator than you will be able to make comparator of any bit size.
We will discuss all 3 operations of “n” bit comparator one by one.
Considers 2 binary numbers A and B both ‘n’ bits wide with its Most Significant Bits (MSBs) An-1 and Bn-1 respectively
Less than
To compare numbers of bit size ‘n’ first, we need to compare its Most Significant Bits (MSB’s).
If An-1 is less than Bn-1 than the whole number A is less than B and the expression would become
(A < B) = A̅n-1 Bn-1 (discussed is single bit comparator, used for A<B)
Note: this is not finished expression
But when MSBs are equal i.e. An-1 equal toBn-1 than we cannot decide whether “Number A” is less than or greater than “B”. then we check the 2nd MSBs i.e. An-2 andBn-2
For which the expression would become:
A̅n-1 B̅n-1 + An-1 Bn-1 (for equality)
A̅n-2 Bn-2 (used for A<B for 2nd MSB)
Overall expression would become
(A<B) = ( A̅n-1 Bn-1 + (A̅n-1 B̅n-1 + An-1 Bn-1 ) A̅n-2 Bn-2
The expression for equality can be represented with ‘X’
(A<B) = A̅n-1 Bn-1 + Xn-1 A̅n-2 Bn-2
If the 2nd MSBs are also equal then the check will be done on 3rd MSB and so on until the last bit. And the expression would become
(A<B) = A̅n-1Bn-1 + Xn-1A̅n-2Bn-2 + Xn-1Xn-2A̅n-3Bn-3+…+Xn-1Xn-2 …X0 A̅0B0 Equation 1
Equal to
The easiest task of the comparator is the equality.
Two numbers “A” and “B” , ‘n’ bits wide are equal when it’s all bits are correspondingly equal.
Equality of a single bit can be achieved by Single XNOR gate. And it’s represented by:
Xn-1 = (An-1 XNOR Bn-1)
Xn-2 = (An-2 XNOR Bn-2)
Xn-3 = (An-3 XNOR Bn-3)
.
.
.
X0 = (A0 XNOR B0)
The output “equal to ” will be true only when all of these above expressions are true.
So the equation for equality will be
(A = B) = Xn-1 n & Xn-2 & Xn-3 &… & X1 & X0 Equation 2
when all the bits of both numbers are equal, then the output will be true otherwise false.
Greater than
“greater than” operation is exactly the same as “less than” operation. The only difference is we have to check for if A is greater than B.
First, we check the MSBs i.e. An-1 and Bn-1.Whose function would be:
(A>B) = An-1 B̅n-1 (discussed is single bit comparator, used for A>B)
and when MSBs are equal i.e. An-1 equal toBn-1 than we cannot decide whether Number “A” is greater than “B” until we check the 2nd MSBs i.e. An-2 and Bn-2
For which the expression would become:
A̅n-1 B̅n-1 + An-1 Bn-1 (for equality)
An-2 B̅n-2 (used for A<B for 2nd MSB)
Overall expression would become
(A>B) = An-1 B̅n-1 + ( A̅n-1 B̅n-1 + An-1 Bn-1)An-2B̅n-2)
The expression for equality can be represented with ‘X’
(A>B) = An-1B̅n-1 + Xn-1An-2B̅n-2
If the 2nd MSBs are also equal than the check will be done on 3rd MSB and so on until the last bit. And the expression would become
(A>B) = An-1B̅n-1 + Xn-1 An-2 B̅n-2 + Xn-1 Xn-2 An-3 B̅n-3+…+ Xn-1 Xn-2 … X0 A0 B̅0 Equation 3
Equation 1,2 and 3 also shows that the terms used in these equations are the product of the output of single bit comparators.
2-bit comparator design is discussed below.
2-Bit Comparator
If we want to design 2-bit comparator all we have to do is put “n=2“ in‘n bits comparator’ equations.
The 3 operations of the 2-bit comparator are given below:
Less than
According to the “n bit comparator” if n=2 then the equation for (A<B) will become”
(A<B) = A̅1B1 + X1A̅0B0
It can be designed with single comparator as:
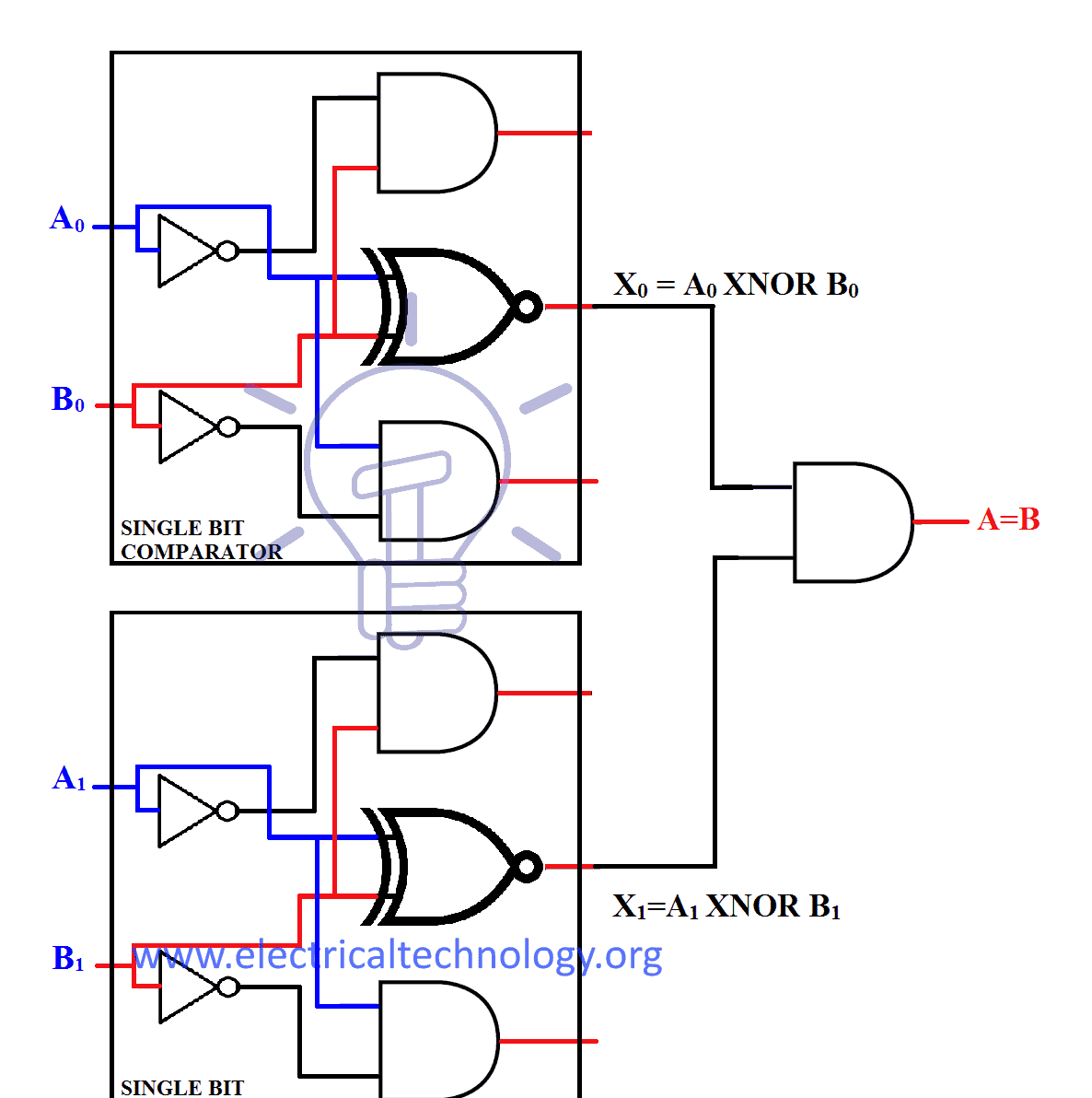
Equal to
According to the “n bit comparator” if n=2 then the equation for (A=B) will become”
(A=B) = X1X0
It can be designed with single comparator as:
Using discrete logic gates:
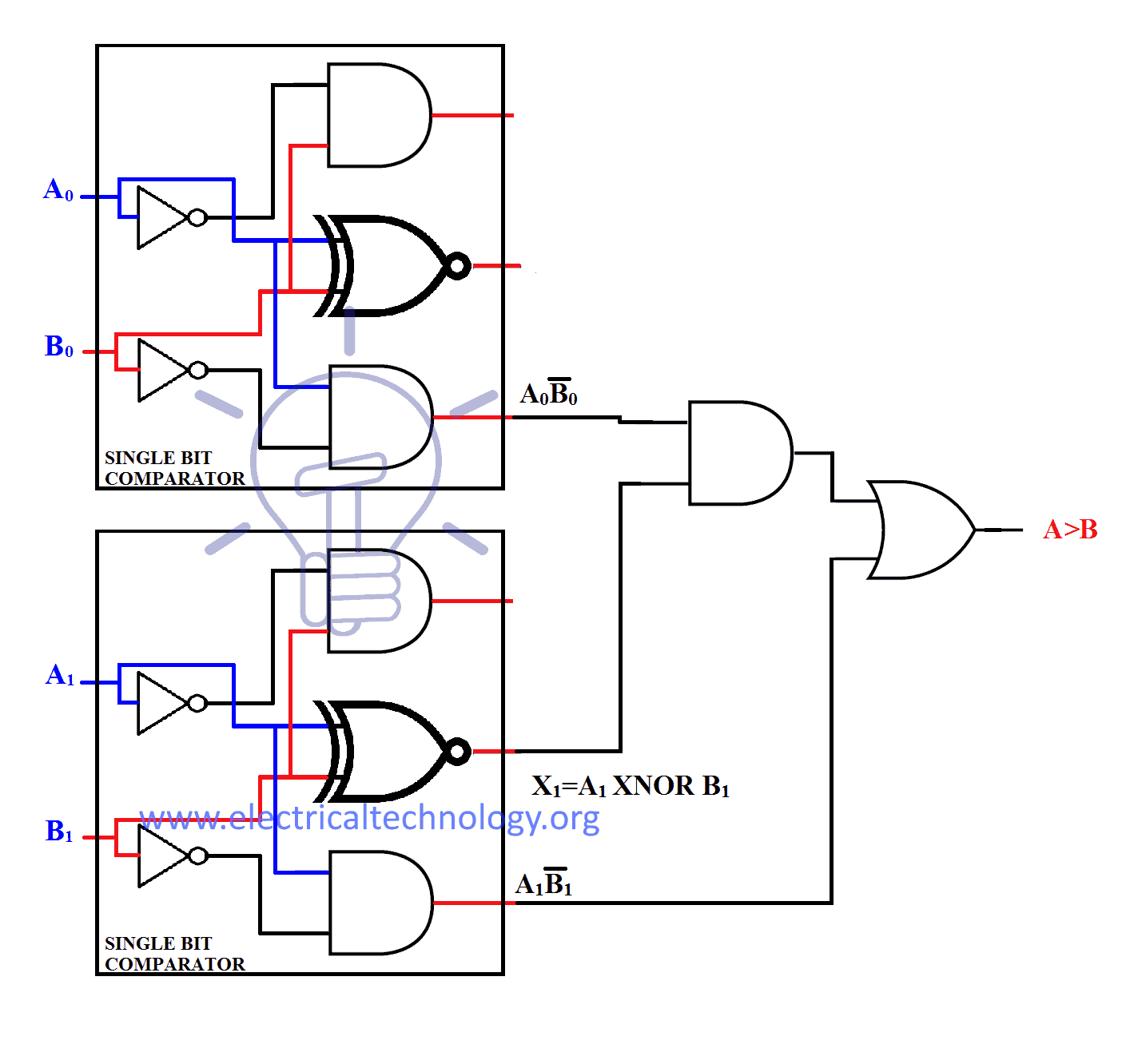
Greater than
According to the “n” bit comparator’s equation if n=2 then the equation for (A>B) will become”
(A>B) = A1 B̅1 + X1 A0 B̅0
It can be designed with single comparator as:
Using discrete logic gates:
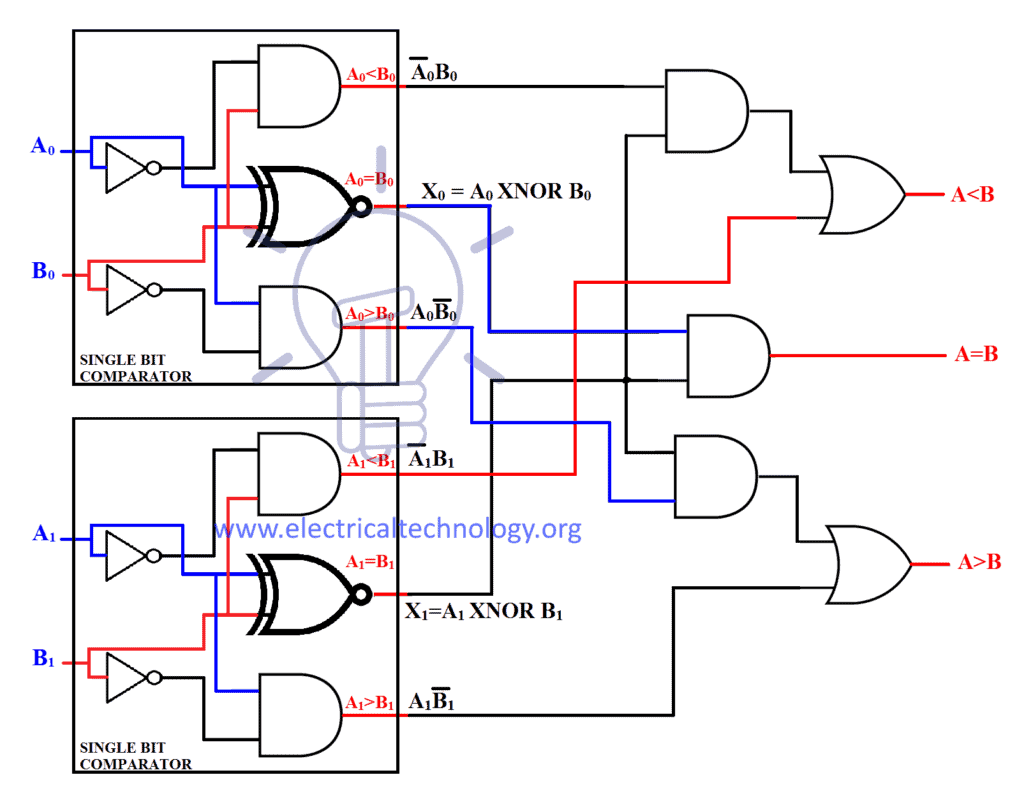
Combined 2-bit comparator
These 3 operations would combine together to form 2-bit comparator as shown below.
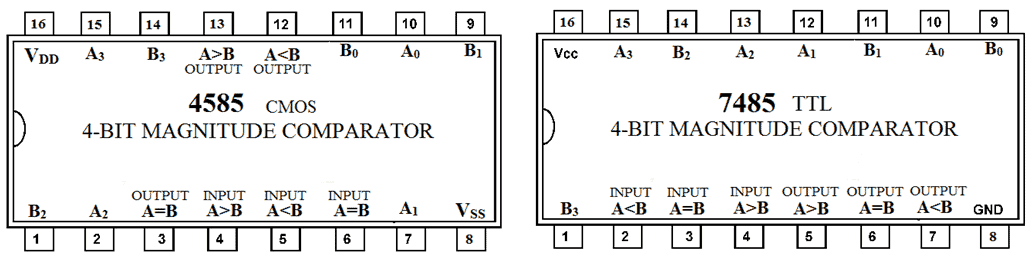
4585 (CMOS) & 7485 (TTL) IC Details
Some of comparators IC with pin configuration is given below.
- 4585 CMOS 4 Bit Magnitude Comparator
- 7485 TTL 4 Bit Magnitude Comparator
Digital Comparators Applications
Comparators are widely used in digital electronics. Some common uses and applications of digital comparators are as follow:
- Comparators are used in microprocessors and CPUs as address decoding circuitry to perform special input/output event for storage devices.
- They are used in biometric and password verification.
- These are also used as process controller in the servo motor.
- Comparators also used in control applications where the binary numbers representing physical variables such as temperature, position, etc. and compared with a reference value.
- They are also used in analog to digital converter i.e. testing meters.
- They are used in some devices that contrast visual images with digital images i.e. computer-aided drafting (CAD) programs
You may also read: