Types of Amplitude Modulation (AM) – Advantages & Disadvantages
Types of Amplitude Modulation with Advantages and Disadvantages
What is Amplitude Modulation (AM) ?
The type of modulation in which the amplitude of the carrier signal varies linearly with respect to the instantaneous amplitude of the message signal is called Amplitude modulation.
Types of Amplitude modulation:
There are several types of Amplitude modulations as follow with their advantages and disadvantages as applications.
- Related Post: Classification and Types of Analog Modulation
Double Sideband Suppressed Carrier(DSB SC)
Introduction
Double sideband is a type of Amplitude modulation in which the frequency spectrum of the message signal is symmetrically situated above & below the carrier signal’s frequency.
The upper & lower frequencies are known as sidebands of the modulated signal. Upper sideband (USB) has frequency components higher than the carrier frequency and the lower sideband (LSB) has lower frequency components than the carrier frequency.
Mathematical Expression:
Suppose the message signal is sinusoidal signal.
m(t) = Amcos ωmt
The carrier signal is a high frequency sinusoidal signal.
c(t) = Ac cos ωct
The Amplitude modulated DSB SC signal will be
ϕDSB-SC(t) = ADSB cos ωct
ADSB = Ac + m(t)
Substituting ADSB
ϕDSB-SC(t) = (Ac + m(t)) cos ωct ……….eq(1)
ϕDSB-SC(t) = Ac cos ωct + m(t) cos ωct
Substituting m(t)
ϕDSB-SC(t) = Ac cos ωct + Amcos ωmt cos ωct
ϕDSB-SC(t) = Ac cos ωct + Am/2 cos (ωm + ωc) t + Am/2 cos (ωm – ωc) t
The modulated signal has three terms.
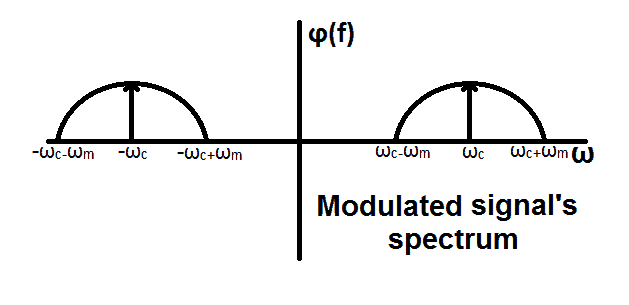
The first term represents the carrier signal. The second term represents the message signal’s frequency shifted to the left by ωc. The third term represents the message signal’s frequency spectrum shifted to the right by ωc as shown in the figure below.
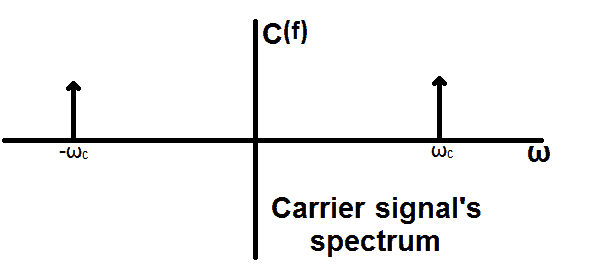
Suppose the message signal’s spectrum is
The spectrum of the carrier signal is
The DSB SC modulated signal’s spectrum is
The message spectrum is centered at ωc having two halves. The upper half (ωc + ωm ) of the message spectrum is called upper sideband & lower half (ωc – ωm ) of the message spectrum is called lower sideband. Because of these two sidebands, it is called double sideband AM transmission.
Modulation Index
In Amplitude modulation, it describes the level of carrier signal amplitude over the level of the message signal.
According to the eq(1)
ϕDSB-SC(t) = (Ac + m(t)) cos ωct
Substituting m(t)
ϕDSB-SC(t) = (Ac + Amcos ωmt) cos ωct
ϕDSB-SC(t) = Ac (1 + Am/Ac cos ωmt) cos ωct
ϕDSB-SC(t) = Ac (1 + μ cos ωmt) cos ωct
where μ= Am/Ac is the modulation index.
Modulation index plays important role in traditional AM discussed in this article below.
- Related Post: What are Industrial Communication Networks? An Overview
Bandwidth
The bandwidth B.W of DSB-SC is the difference between the maximum and minimum frequency of the modulated signal.
B.W = (fc+ fm) – (fc– fm )
B.W = fc+ fm – fc+ fm
B.W = 2 fm
The bandwidth of the DSB-SC modulated signal is twice the bandwidth of the message signal.
Demodulation
Demodulation is the process of acquiring the original signal (message signal) from the modulated signal (received signal).
To demodulate a DSB-SC signal, it is multiplied with the carrier signal (coherent frequency).
Assume the modulated signal is
ϕ(t) = m(t) cos ωct
Then the modulated signal will be
e(t) = m(t) cos ωct cos ωct
e(t) = ½ m(t) (1 + cos 2ωct)
e(t) = ½ m(t) +½ m(t) cos 2ωct
The demodulated signal contains two terms, a message signal and a high frequency term. The high frequency term is filtered out by passing through Low Pass Filter.
Advantages:
- The modulation process is very simple
- No need for filtering during modulation for sidebands.
Disadvantages
- Demodulation need coherent carrier source.
- It carrier less information about the carrier.
- Carrier power is wasted
- Envelop detection is not possible.
- High bandwidth compares to SSB, VSB.
Related Post: Phase Locked Loop- its Operation, Characteristics & Application
Double side-band full carrier (Traditional Amplitude Modulation)
Introduction
In DSB-FC, the carrier signal is utilized during demodulation. The message signal is stored in the envelope of the modulated signal. In order to acquire this envelope, the amplitude of the message signal in the modulated signal should not go below Zero. i.e.
Ac + m(t) ≥ 0
carrier amplitude Ac should be adjusted to satisfy the equation.
Ac – Am ≥ 0
Am = lowest peak amplitude of the message signal.
Ac ≥ Am
1 ≥ Am/ Ac
1 ≥ μ
where μ = Am/ Ac
0 ≥ μ ≥ 1
Thus the modulation index μ should be between 0 & 1 for envelope detection at the receiver.
Demodulation:
DSB-FC or traditional AM can be demodulated by using a coherent source or envelope detector. Envelop detector is a very simple and inexpensive process.
An envelope detector is a simple diode, capacitor and resistor circuit. It does not need any coherent source or any low pass filter.
The message signal is rectified out using this envelope detector.
Advantages
- The receiver is very simple and low cost.
- Broadcasting is very efficient.
Disadvantages
- Waste too much power.
- Overall low efficiency (about 33%).
- AM is affected by noise.
Quadrature Amplitude Modulation (QAM)
Quadrature Amplitude Modulation is the type of Amplitude modulation in which two different message signals are transmitted on the same frequency carrier with a different phase shift.
The DSB modulated signal has double bandwidth of the modulating signal. To overcome excessive bandwidth, QAM is applied by sending two message signals on the same frequency carrier signal with 90° phase difference.
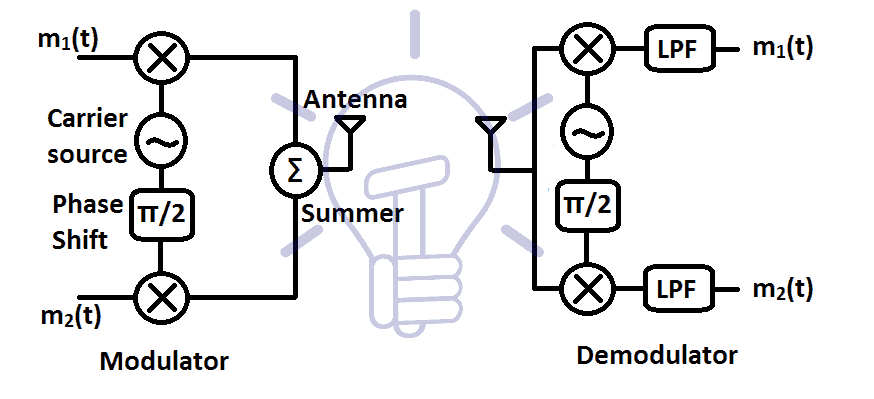
Block Diagram
The block diagram of QAM is given below:
This block diagram shows the modulation of two message signals. The carrier source produces carrier signal. The carrier signal with 0° phase shift is used with the first message signal m1(t) and the carrier signal with 90° phase shift is used with the second message signal m2(t). Both modulated signals are then added using summer to make a single signal having same frequency and bandwidth.
- Related Post: What is GSM and How does it Work?
Mathematical expression
Suppose two message signals are m1(t), m2(t)
The carrier signal is
c(t)= cos ωct.
So the 90° degree phase shifted signal of c(t) will be
c(t)= cos (ωc+90°)t = sin ωct.
So the modulated single will be
ΦQAM(t) = m1(t) cos ωct + m2(t) sin ωct
Demodulation
QAM modulated signal cannot be demodulated using envelope detection technique because it contains two message signals. The messages signals are demodulated by multiplying the QAM signal with its coherent carrier signal as follows.
To get m1(t), the received signal is multiplied with cos ωct.
e(t)= (m1(t) cos ωct + m2(t) sin ωct) cos ωct
e(t)= m1(t) cos2 ωct + m2(t) sin ωct cos ωct
e(t)= ½ m1(t) (1+cos 2ωct) + ½ m2(t) sin 2ωct
e(t)= ½ m1(t) +½ m1(t) cos 2ωct) + ½ m2(t) sin 2ωct
By passing through Low Pass Filter
e(t)= ½ m1(t)
To get m2(t), the received signal is multiplied with sin ωct.
e(t)= (m1(t) cos ωct + m2(t) sin ωct) sin ωct
e(t)= m1(t) cos ωct sin ωct + m2(t) sin2 ωct
e(t)= ½ m1(t) sin 2ωct + ½ m2(t) (1-cos 2ωct)
e(t)= ½ m1(t) sin 2ωct + ½ m2(t) – ½ m2(t) cos 2ωct)
By passing through Low Pass Filter
e(t)= ½ m2(t)
Advantages
- Can carry more than one message signal.
- Utilize low bandwidth as compared to the information transmitted.
Disadvantages
- It has a complex design of transmitter and receiver.
- Envelope detection technique does not work.
Related Post: Carrier Acquisition, Need for Carrier Acquisition & Techniques
Single sideband (SSB)
The type of Amplitude modulation, in which only single sideband is transmitted through an antenna is called single sideband communication.
Unlike DSB, the SSB modulated signal has only single side-band either upper side-band (usually) or lower side-band.
The SSB modulated signal is made from DSB signal by passing it through a bandpass filter. The bandpass filter cutoff the DSB modulated signal at ωc and filter out either upper sideband or lower sideband as shown in fig below.
Bandwidth
The bandwidth of the SSB signal is equal to the bandwidth of the message signal.
Demodulation
If the received signal is SSB suppressed carrier signal then the demodulator needs a coherent source. which generates the same frequency carrier as the received signal. After demodulation, the signal is passed through low pass filter to filter out high-frequency components.
If the received signal is SSB full carrier signal then it is best to use an Envelope detector or Rectifier. The SSB full carrier transmission is a type of SSB transmission in which the carrier amplitude is very large compared to message signal amplitude.
Advantages
- Bandwidth is equal to message signal.
- Save half power by transmitting one sideband.
Disadvantages
- Filtering one sideband is very difficult and add complexity to the transmitter circuit
- It needs a bandpass filter with a very sharp cutoff. An ideal filter.
Related Post: Quantization & Sampling? Types & Laws of Compression
Vestigial sideband (VSB)
As we know that a real bandpass filter does not have a sharp cutoff and it does not filter all the frequencies outside of the cutoff region. A real filter allows some frequency content outside of the cutoff region. Because of this problem vestigial sideband is implemented.
In VSB, one sideband and a little portion (25%) of the second sideband is transmitted as shown in the figure below.
Bandwidth
The bandwidth of VSB modulated signal is greater than SSB but it is lower than the DSB modulated signal. The bandwidth of the VSB modulated signal is 25% greater than the bandwidth of the message signal.
B.W = fm + 25% fm
Demodulation
If the received signal is VSB suppressed carrier signal, then the demodulation only needs coherent carrier source. The rest of the demodulation process is same as SSB and DSB suppressed carrier demodulation.
If the received signal is VSB with the carrier, then an envelope detector can also demodulate the signal. The VSB full carrier needs very large carrier amplitude as compared to message signal’s amplitude.
Related Posts:
- Basic Electronics Engineering Interview Questions & Answers
- Introduction to Signals, Types, Properties, Operation & Application











it is nace ilike it but you have to be add wave form also if it has