Star Connection (Y): Three Phase Power, Voltage & Current Values
Three Phase Star Connection: Line, Phase Current, Voltages & Power in Y Configuration
What is Star Connection (Y)?
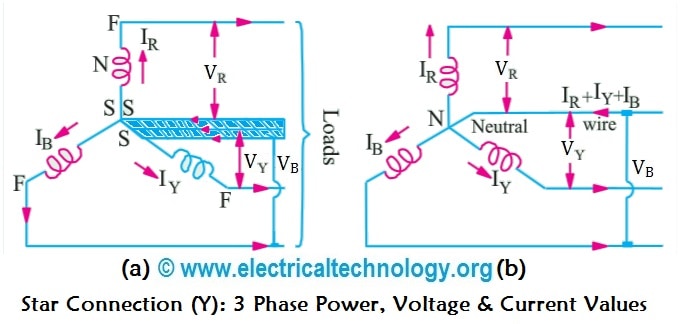
Star Connection (Y) System is also known as Three Phase Four Wire System (3-Phase 4 Wire) and it is the most preferred system for AC power distribution while for transmission, Delta connection is generally used.
In Star (also denoted by Y) system of interconnection, the starting ends or finishing ends (similar ends) of three coils are connected together to form the neutral point. Or
Star Connection is obtained by connecting together similar ends of the three coils, either “Starting” or “Finishing”. The other ends are joined to the line wires. The common point is called the neutral or Star Point, which is represented by N. (As shown in fig 1)
Star Connection is also called Three Phase 4 wires (3-Phase, 4-Wires) system.
Also Read:
- Delta Connection (Δ): 3 Phase Power, Voltage & Current Values
- Difference Between Star (Y) and Delta (Δ) Connections
If a balance symmetrical load is connected across three phase voltage system in parallel, then the three currents will flow in neutral wire which quantities would be same, but they would be differ by 120° (out of phase), hence the vector sum of these three currents = 0. i.e.
IR + IY + IB = 0 ……………. Victorially
The voltage between any two terminals or voltage between Line and Neutral (Star Point) is called Phase voltage or Star voltage denoted by VPh. And the voltage between two Lines is called Line to Line Voltage or Line Voltage denoted by VL.
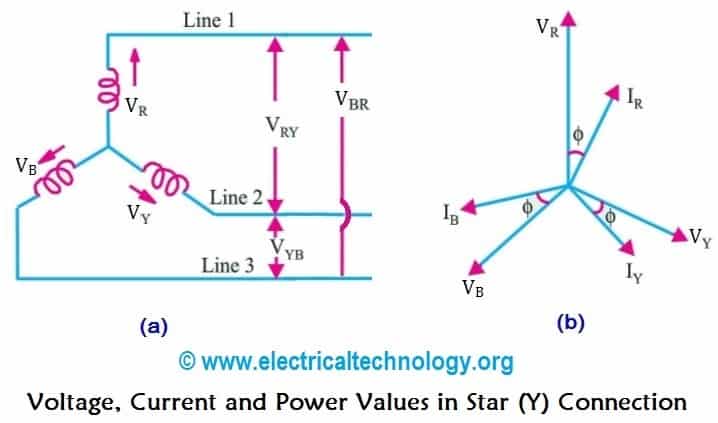
Voltage, Current and Power Values in Star Connection (Y)
Now we will find the values of Line current, Line Voltage, Phase Current, Phase Voltages and Power in three phase Star AC system.
Line Voltages and Phase Voltages in Star Connection
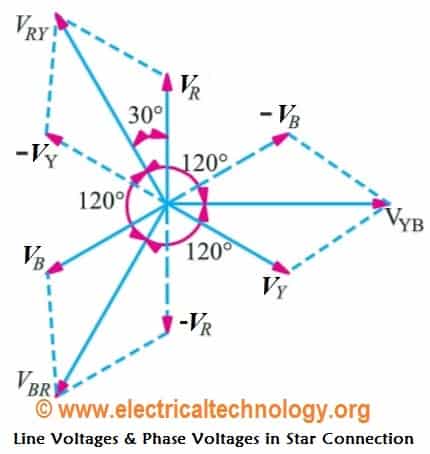
We know that the Line Voltage between Line 1 and Line 2 (from fig 3a) is
VRY = VR – VY …. (Vector Difference)
Thus, to find vector of VRY, increase the Vector of VY in reverse direction as shown in the dotted form in the below fig 2. Similarly, on the both ends of vector VR and Vector VY, make perpendicular dotted lines which look like a parallelogram as shown in fig (2). The Diagonal line which divides the parallelogram into two parts, showing the value of VRY. The angle between VY and VR vectors is 60°.
Hence, if
VR = VY = VB = VPH
then
VRY = 2 x VPH x Cos (60°/2)
= 2 x VPH x Cos 30°
= 2 x VPH x (√3/2) …… Since Cos 30° = √3/2
VRY = √3 VPH
Similarly,
VYB = VY – VB
VYB = √3 VPH
And
VBR = VB – VR
VBR = √3 VPH
Hence, it is proved that VRY = VYB = VBR is line voltages (VL) in Star Connection, Therefore, in Star Connection;
VL = √3 VPH or VL = √3 EPH
It is seen from the fig 2 that;
- Line voltages are 120° apart from each other
- Line voltages are 30° leading from the corresponding phase voltages
- The angle Ф between line currents and respective line voltages are (30°+Ф), i.e. each line current is lagging (30°+Ф) from the corresponding line voltage.
Related Post: Star and Delta Connected Lighting Loads
Line Currents and Phase Currents in Star Connection
It is seen from fig (3a) that each line is in series with individual phase winding, therefore, the value of line current is same as in Phase windings to which the line is connected. i.e.;
- Current in Line 1 = IR
- Current in Line 2 = IY
- Current in Line 3 = IB
Since, the flowing currents in all three lines are same, and the individual current in each line is equal to the corresponding phase current, therefore;
IR = IY = IB = IPH …. The phase current
Line Current = Phase Current
IL = IPH
In simple words, the value of Line Currents and Phase Currents are same in Star Connection.
- Also read : Three Phase Current Values in a 3-Phase System
Power in Star Connection
In a three phase AC circuit, the total True or Active power is the sum of the three phase power. Or the sum of the all three phase powers is the Total Active or True Power.
Hence, total active or true power in a three phase AC system;
Total True or Active Power = 3 Phase Power
Or
P = 3 x VPH x IPH x CosФ ….. Eq … (1)
We know that the values of Phase Current and Phase Voltage in Star Connection;
IL = IPH
VPH = VL /√3 ….. (From VL = √3 VPH)
Putting these values in power eq……. (1)
P = 3 x (VL/√3) x IL x CosФ …….…. (VPH = VL /√3)
P = √3 x√3 x (VL/√3) x IL x CosФ ….… {3 = √3x√3}
P = √3 x VL x IL x CosФ
Hence proved;
Power in Star Connection,
P = 3 x VPH x IPH x CosФ or
P = √3 x VL x IL x CosФ
The same is explained in 3-Phase Circuit MCQs with explanatory Answer (MCQs No.1)
Similarly,
Total Reactive Power = Q = √3 x VL x IL x SinФ
Where Cos Φ = Power factor = the phase angle between Phase Voltage and Phase Current and not between Line current and line voltage.
Good to know: Reactive Power of Inductive coil is taken as Positive (+) and that of a Capacitor as Negative (-).
Also, the total apparent power of the three phases;
Total Apparent Power = S = √3 x VL x IL Or,
S = √ (P2 + Q2)
Also Read :
- Introduction to Series, Parallel and Series-Parallel Connections
- Series, Parallel and Series-Parallel Connection of Batteries
- Three Phase Motor Connection STAR/DELTA Without Timer. Power & Control Diagrams
- Star Delta 3-phase Motor Automatic starter with Timer





This is the best way to learn. I have learn a lot of topics
Very helpful artical..it explains the topic very clearly…
Thanks..
Explained very clearly about connection of networks. Thanks.