How to Determine the Number of Nodes, Loops, Branches & Meshes in a Circuit?
What is Node, Branch, Loop and Mesh in an Electric Circuit, and How to Identify them?
Understanding the fundamentals of electric circuits and networks is crucial for solving and analyzing complex systems using network theorems. Four key elements and terms in this process are Nodes, Branches, Loops, and Meshes.
In this tutorial, we will explore the roles of Nodes, Branches, Loops, and Meshes in electrical circuits, followed by methods to determine their quantities. This knowledge enables us to apply circuit-solving techniques to simplify complex networks.
Let’s break down these concepts step by step.
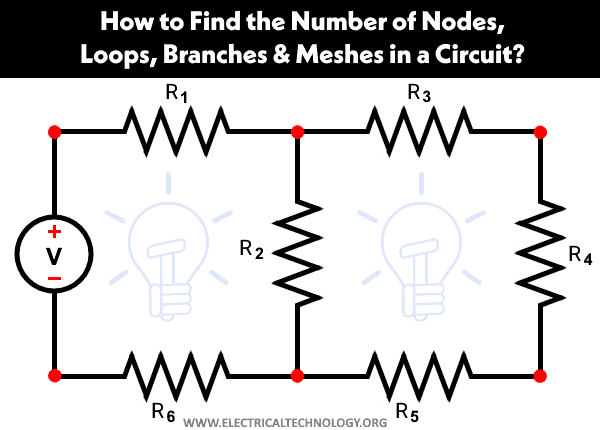
First, we’ll consider a simple electric circuit illustrated in fig-1, comprising 7 components.
Node
A point or junction where two or more elements of a circuit (such as resistors, capacitors, inductors, etc.) meet is called a Node. In other words, a Node is a point of connection between two or more branches.
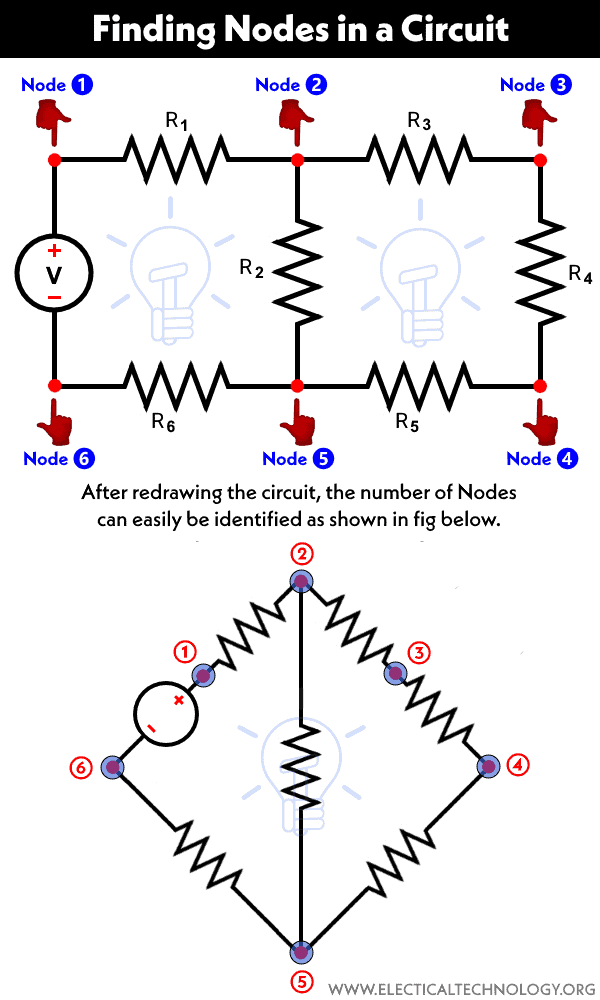
Finding Nodes in an Electric Circuit
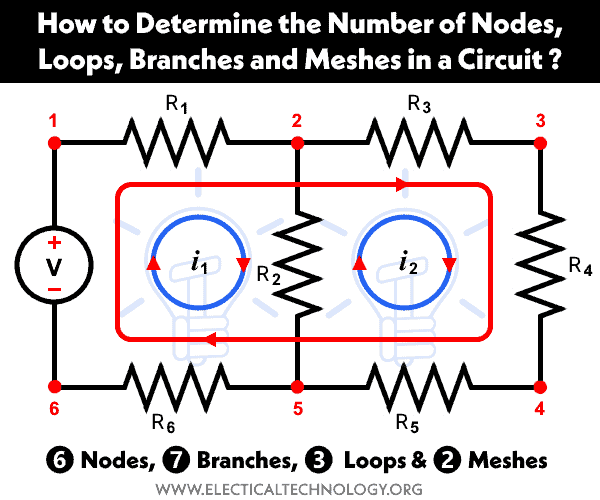
After redrawing the circuit shown in fig-1 above, we obtain the equivalent circuit shown below. Now, let’s determine the number of nodes. As illustrated in fig-2, there are 6 nodes.
Branch
A part or section of a circuit located between two junctions is called a branch. Within a branch, one or more elements with two terminals can be connected. In other words, it may consist of any two terminals connected by a single component, such as a voltage source, current source, resistor, etc.
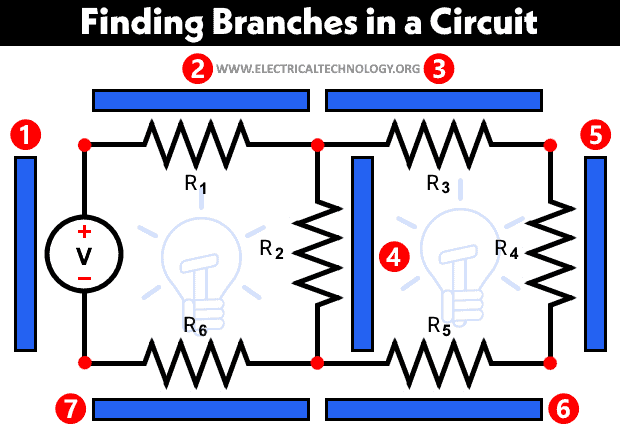
Finding Branches in an Electric Circuit
The circuit shown in figure-3 consists of seven branches, which include a voltage source denoted by “V” and six resistors. Each branch is represented by a blue-colored horizontal bar over it.
Loop
A closed path within a circuit containing more than two meshes is referred to as a loop. In other words, a loop can encompass multiple meshes, but a single mesh cannot contain more than one loop. Put simply, a mesh represents a closed path within a circuit.
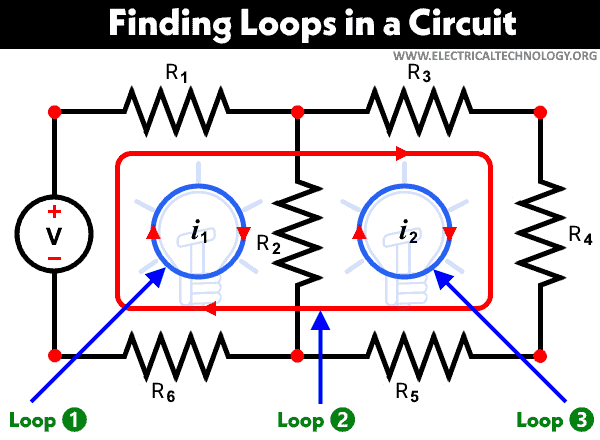
Finding Loops in an Electric Circuit
The number of loops in a circuit can be determined using the fundamental theorem of circuit and network topology.
l = b – n + 1
Where:
- l = Number of Loops
- b = Number of branches
- n = Number of nodes
Therefore, there are 2 independent loops, and the total number of loops is 3 in fig-4.
Mesh
A closed loop that doesn’t contain any other loop within it is referred to as a mesh. In other words, any path within a circuit that doesn’t include any other path is considered a mesh.
Finding Meshes in an Electric Circuit
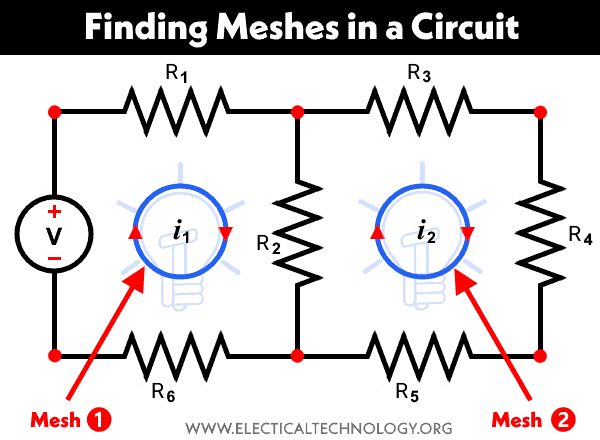
Using this definition, there are two meshes in the circuit illustrated in fig-5.
The overall circuit depicted in fig-1 comprises 6 Nodes, 7 Branches, 3 Loops, and 2 Meshes, as illustrated in fig-6.
Related Posts:
- What is an Electric Circuit? Types of Circuits, Network & Parts Of Circuit
- The Main Difference between Linear and Nonlinear Circuit
- Difference between Unilateral and Bi-Lateral Circuits & Elements
- Difference between Active and passive Components
- Difference Between Current and Voltage
- Difference between AC and DC (Current & Voltage)
- What is Electric Current, its Unit, Formula, Types & Applications
- What is Voltage? its Unit, Formula, Types & Applications
- What is Resistance? Resistivity (ρ) & Specific Resistance Ω.
- What is Electrical Power? Types of Electric Power and their Units
- What is Electrical Energy? Its Unit, Formula & Applications
- What is Electricity? Types, Sources & Generation of Electricity
- What is Volt (V)? Unit in Electrical Engineering and Physics
- What is Ampere (A)? Unit in Electrical Engineering & Physics






Or B = N + 1 i.e. Branches = Nodes + 1
e.g. Nodes = Branches – 1 i.e. N = B – 1
Branch
That the terms junction or point mean one and the same must be emphasized.
Above it says there are 3 loops in the circuit. But if you apply the loop formula L=B-N+1,we get
Loop= 7-6+1= 2 loops ,why??? Am i missing something here?
I was thinking of the same thing too
Hi there,
Formula “L = B – N + 1” is used to find the number of independent loops which are 2. The total number of loops are three.
when using the formula, you will be using only the independent loop and that’s 2 loops . The third loop is dependent on the other two and isn’t used in the formula.
Hello, I don’t understand the equation for finding out the number of loops as the equation is l = b- n + 1 but there are 6 branches, 6 nodes so the number of loops should be 1 no? Could anyone explain how the number of loops is 3 instead please?
Formula “L = B – N + 1” is used to find the number of independent loops which are 2. The total number of loops are three.