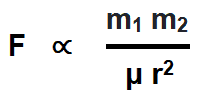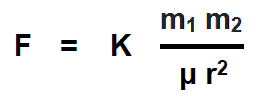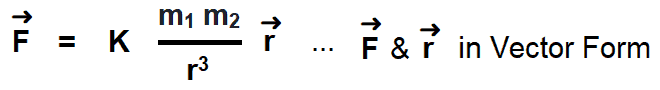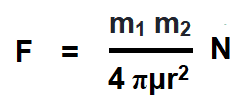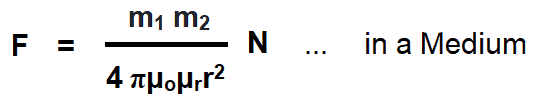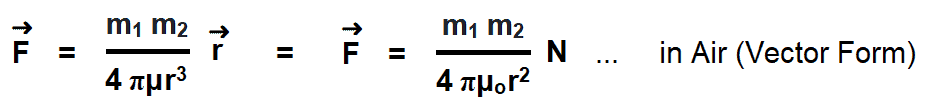Coulomb’s Laws of Magnetic Force – Formula & Solved Example
Coulomb’s Law of Magnetic Force
Charles-Augustin de Coulomb was the first French physicist and military engineer who introduced the Laws of Magnetic Force in 1785 known as Coulomb’s Inverse Square Law of magnetic force or Coulomb’s Law of magnetic force. He represented the quantitative expression of force for two isolated point poles.
Keep in mind that it is not possible to practically get an isolated pole because even a tiny piece of magnet has two poles namely S (south) and N (north) poles. The concept of isolated poles is just a theoretical approach which does not relate to any experience or practice. In practical applications, the poles of long and tiny magnets are supposed to be point poles.
Coulomb’s 1st & 2nd Laws of Magnetic Force
Thus, Coulomb found the law of magnetic force for two magnetic masses by using the torsion balance (an instrument used to measure very small forces). Coulomb’s laws of magnetic force can be stated as follow:
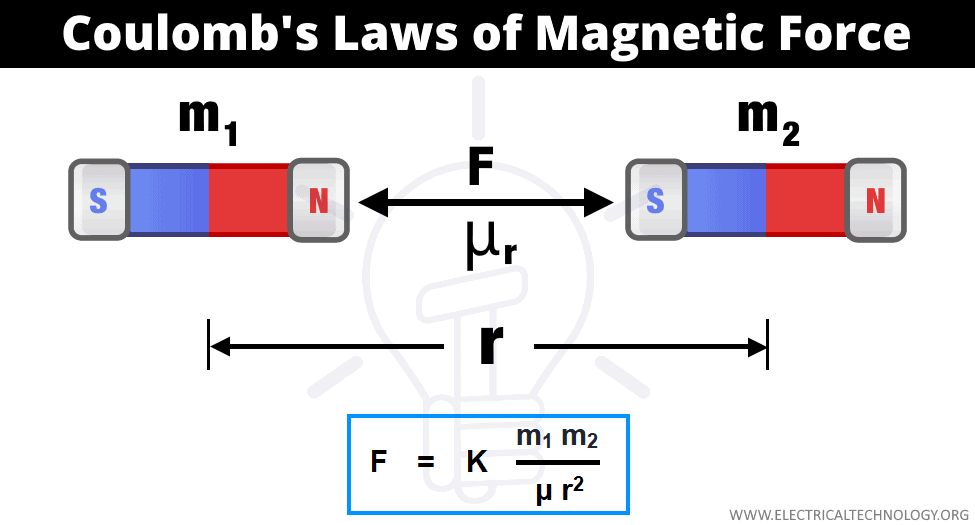
The force (repulsion or attraction) between two magnetic poles (in a medium) is directly proportional to the product of their poles strength and inversely proportional to the square of the distance between them.
In other words,
Coulomb’s Laws of magnetic force stats that the force of attraction or repulsion between two magnetic poles placed in medium is:
- Directly proportional to their poles strength (F ∝ m1m2).
- Inversely proportional to the square of the distance “r2” between poles.
- Inversely proportional to the absolute permeability “μo” of the surrounding medium.
Mathematically,
- F ∝ m1m2 and F ∝ 1/r2
- F = K (m1m2) / μr2
Related Posts
Coulomb’s Law of Magnetic Force Formulas & Explanation
Suppose;
- Magnetic strength of the magnetic poles = m1 and m2.
- Distance between two magnetic poles = r
- Permeability of the medium = μ
Then, the force “F” of attraction or repulsion between two magnetic poles would be:
or
or
Here, the r̂ is a unit vector which shows the direction of “r”. So,
The value of constant “K” in the SI unit system is K = 1/4π.
or
In vector form,
In the above equation, If m1 = m2 = m and “r” is one meter, then
Then, m2 = 1 or m = ±1 weber (see note below).
The unit of weber (a unit of magnetic flux i.e. a flux density of one Wb/m2 e.g. one weber per meter square = 1 Tesla) named after the German Physicist Wilhelm Edward Weber where one weber = 1 volt / second or 108 Maxwell’s (centimeter-gram-second equal to the magnetic flux through 1 square centimeter in a magnetic field or one Gauss (centimeter-gram-second unit of magnetic induction).
Hence, a unit of magnetic pole may be defined as that pole which when placed in vacuum at a distance of one meter from a similar and equal pole repels it with a force of 1/4 πμo newtons.
Therefore, a unit magnetic pole may be defined as:
A pole placed in a vacuum repels the equal and similar pole with a force of 1/4 πμo Newtons if the distance between them are 1 meter is known as a unit magnetic pole.
or
A unit magnetic pole is defined as the magnetic pole which when placed at a distance of one meter from a very long straight conductor carrying a current of one ampere experiences a force of 1/2π newtons.
Related Posts:
Solved Example on Coulomb’s Law of Magnetic Force
Example:
a square cross-sectional magnet has a pole strength of 3×10-3 webers and a cross-sectional area of 5 cm x 5cm. Calculate the strength at a distance of 50 cm from the pole in air.
Solution:
Given data:
- Pole strength = 3 x 10-3 wb
- distance = 50 cm or 0.25 m
- Field strength = H ?
Field Strength H =
Putting the values
H = 760 N/Wb
Good to Know:
- Permeability (μ): The ability of concentrating the magnetic or electromagnetic flux in a medium is called permeability. It is represented by the symbol of my or mu or micro “μ“. The more the permeability of a material, the more strong a magnetic field can be produced in it. Each medium has two permeabilities namely absolute permeability (μo) and relative permeability (μr).
μ = μo μr
The ferromagnetic materials (e.g. Iron, Steel, Nickle, Cobalt and their alloys) have high permeability as compared to vacuum.
- Absolute Permeability (μo): The ratio of B/H for a magnetic field in a vacuum in weber per meter square (Wb/m2) is called the absolute permeability (i.e. for non space e.g. air) . Where “B” is flux density and “H” is the magnetizing force.
μo = B/H = μo μr
The reference value of absolute permeability in a vacuum is μo = 4π x 10-7.
- Relative Permeability (μr): It is the ratio of the absolute permeability “μ” of a material to the absolute permeability “μo“.
In other words, the ratio of the permeability of a material to that of free space is called related permeability or the relative permeability of a material is the ratio of its absolute permeability to the permeability of a vacuum.
μr = μ / μo
Alternatively, the relative permeability of a material is the ratio between the produced flux density “B” in that material and the flux density produced by same magnetizing force “H” in the vacuum.
μr = B (Material) / Bo (Vacuum) … For same H (Magnetizing force)
The value of μr in space and air is unity (1) i.e. μr = 1. There is no unit for relative permeability as it is a ratio between permeability and absolute permeability.
In
- Coulomb’s Law or magnetic force is related to magnetism and electromagnetism (i.e. inductors, coils, solenoid etc.)
- Coulomb’s Law or laws of electrostatic is related to the static electricity and capacitors (static charge)
- Faraday’s Law of electromagnetic induction is related to static and dynamic induced EMF, magnetism and generation of electricity in alternator.
Related Posts:
-
- Kirchhoff’s Current & Voltage Law (KCL & KVL) | Solved Example
- Ohm’s Law with Simple Explanation
- Electric & Magnetic Flux, Density & Field Intensity Formulas
- Formula & Equations for Ohm’s, Kirchhoff’s & Coulomb’s Laws
- Norton’s Theorem. Easy Step by Step Procedure with Example
- Thevenin’s Theorem. Step by Step Procedure with Solved Example