Binary Multiplier – Types & Binary Multiplication Calculator
Digital Binary Multiplier & Binary Multiplication Calculator
What is Digital Binary Multiplier?
A binary multiplier is a combinational logic circuit or digital device used for multiplying two binary numbers. The two numbers are more specifically known as multiplicand and multiplier and the result is known as a product.
The multiplicand & multiplier can be of various bit size. The product’s bit size depends on the bit size of the multiplicand & multiplier. The bit size of the product is equal to the sum of the bit size of multiplier & multiplicand.
Binary multiplication method is same as decimal multiplication. Binary multiplication of more than 1-bit numbers contains 2 steps. The 1st step is single bit-wise multiplication known as partial product and the 2nd step is adding all partial products into a single product.
Partial products or single bit products can be obtained by using AND gates. However, to add these partial products we need full adders & half adders.
The schematic design of a digital multiplier differs with bit size. The design becomes complex with the increase in bit size of the multiplier.
Also read:
- Binary Encoder – Construction, Types & Applications
- Binary Decoder – Construction, Types & Applications
Types of Binary Multipliers
- 2×2 Bit Multiplier
- 3×3 Bit Multiplier
- 4×4 Bit Multiplier
lets discuss one by one as follow:
2×2 Bit Multiplier
This multiplier can multiply two numbers having bit size = 2 i.e. the multiplier and multiplicand can be of 2 bits. The product bit size will be the sum of the bit size of the input i.e. 2+2=4. The maximum range of its output is 3 x 3 = 9. So we can accommodate decimal 9 in 4 bits. It is another way of finding the bit size of the product.
Suppose multiplicand A1 A0 & multiplier B1 B0 & P3 P2 P1 P0 as a product of the 2×2 multiplier.
First, multiplicand A1A0 is multiplied with LSB B0 of the multiplier to obtain the partial product. This is obtained using AND gates. Then the same multiplicand is multiplied (AND) with the 2nd LSB to get the 2nd partial product. The multiplicand is multiplied with each bit of the multiplier (from LSB to MSB) to obtain partial products.
The number of partial products is equal to the number of bit size of the multiplier. In 2×2 multiplier, multiplier size is 2 bits so we get 2 partial products.
Now we need to add these partial products. There are two ways of adding;
- Using 2-bit full adder
- Using individual single bit adders.
Also read:
- MUX – Digital Multiplexer | Types, Construction & Applications
- DEMUX – Demultiplexer | Types, Construction & Applications
2×2 Bit Multiplier using 2-Bit Full Adder
if we use 2-bit full adder all we have to do is to know which term should be added.
The partial product of LSBs of inputs is the LSB of the product. So it should remain untouched.
The other terms of each partial product should be considered and added using 2-bit full adder.
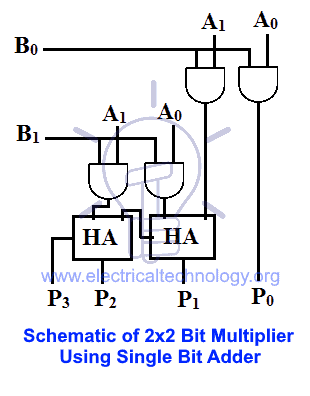
Construction and design schematic of 2×2 bit multiplier is given in the figure below;
The single bit from LSB partial product, 2 bits from the Sum & a carry bit makes the 4 bits of the products.
Truth Table for 2 Bit Multiplier
| Multiplier Bits | Multiple of Multiplicand | ||
| Yi+1 | Y1 | Multiples | Implementation |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | x |
| 1 | 0 | 2 | Shift left X by 1 |
| 1 | 1 | 3 | (Shift left X by 1) + X |
2×2 Bit Multiplier using Individual Single Bit Adders
Single bit adders can be half adder & full adder. The difference between half adder & full adder is that half adder can only add 2 numbers and full adder can add 3 numbers including the carry in from previous addition.
However, in this condition, we only need half adder because the numbers to be added are only 2.
Schematic of 2×2 bit multiplier using single bit adder is given in the figure below.
- Ring Counter & Johnson Counter – Construction & Operation
- Digital Flip-Flops – SR, D, JK and T Flip Flops
3×3 Bit Multiplier
This multiplier can multiply two numbers having a maximum bit size of 3 bits. The bit size of the product will be 6. The maximum range of its product is 7 x 7 = 49. It can be accommodated in 6 bits which is the size of its output product.
Suppose multiplicand A2 A1 A0 & multiplier B2 B1 B0 & product as P5 P4 P3 P2 P1 P0.
There are 3 partial products in this multiplication because there is a 3-bit multiplier. These 3 partial products will be added using any of the two methods;
- Using 3-bit full adder
- Using individual single bit adders.
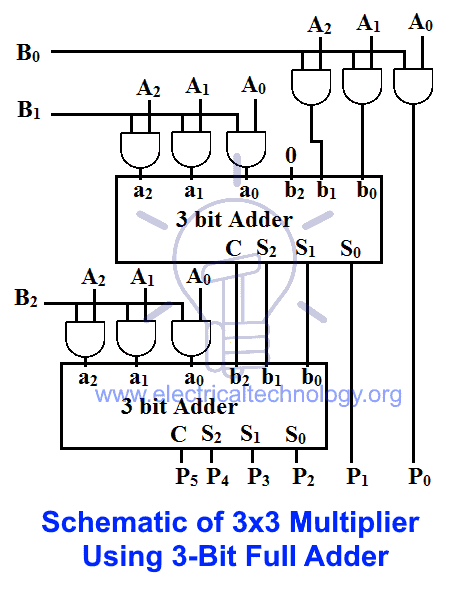
3×3 Bit Multiplier using 3-Bit Full Adder
This method is easy compared to the other method. We only have to use two 3-bit full adders to add these 3 partial products.
The LSB of the first partial product should not be touched. It will flow out as LSB of Product.
The first two partial products should be added together using 3-bit full adder. Then the sum of that adder should be added to the third partial product using another full adder.
While adding these partial products, the LSB of the sum of each adder should be routed directly as output and the remaining 3 bits of the sum should be added to the next partial product.
The schematic of 3×3 multiplier using 3-bit full adder is given below;
3×3 Bit Multiplier using Single-Bit Adders
We need 9 AND gate for partial products and 3 Half adders & 3 full adders.
The schematic of 3×3 multiplier using single-bit adder is given below;
As you can see, each term is added to each other & the carry bits are sent to the next adders on the left side.
4×4 Bit Multiplier
This multiplier can multiply a binary number of 4-bit size & gives a product of 8-bit size because the bit size of the product is equal to the sum of bit size of multiplier and multiplicand. The maximum number it can calculate us 15 x 15 = 225. You can also evaluate the number of bits from the maximum output range.
Suppose multiplicand A3 A2 A1 A0 & multiplier B3 B2 B1 B0 & product as P7 P6 P5 P4 P3 P2 P1 P0 for 4×4 multiplier.
In 4×4 multiplier, there are 4 partial products and we need to add these partial products to get the product of multiplier.
They can be added using 4-bit full adders or single bit adders (half-adder & full-adder). The design using Single bit adders is very complicated compared to using 4-bit full adders.
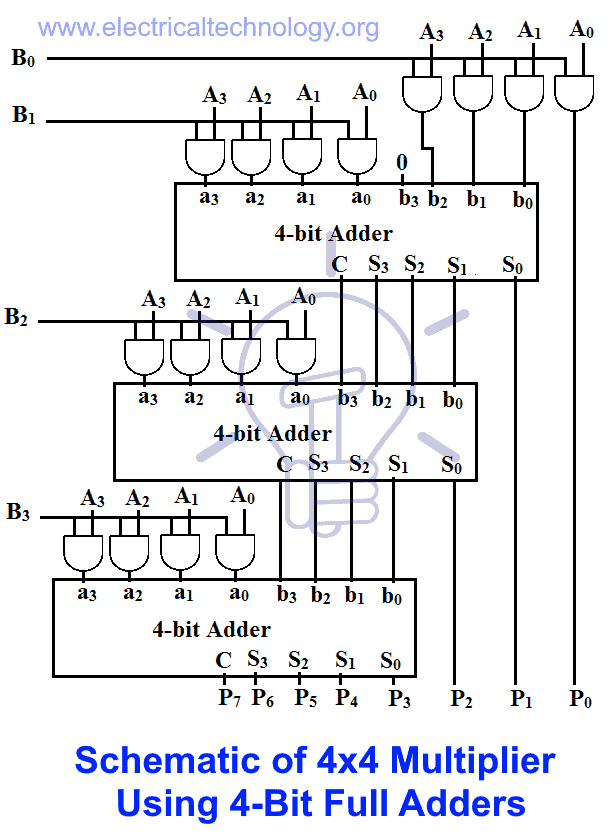
4×4 Bit multiplier using 4-Bit Full Adders
The implementation of 4×4 multiplier using 4-bit full adders is same as implementing a 3×3 multiplier.
Schematic of 4×4 bit multiplier using 4-bit full adders is given below.
The LSB of the first partial product is the LSB of product, so it will flow out directly to the output. The LSB of the sum of each adder is taken as a bit of product and the rest of the sum bits are added with the next partial products.
Binary Multiplication Calculator
Below is a Binary Multiplication Calculator which performs two main and related functions i.e. it will show the result for binary multiplication in binary as well as equivalent decimal. For binary multiplication, you have to enter the values in binary format (i.e. 1011010) in both input fields. Click on calculate to show the result and binary multiplication in binary and decimal as well.
Binary Number Multiplication (Binary Multiplier) calculator
You may also read:
- Logic NOT Gate – Digital Inverter Logic Gate
- Digital Logic OR Gate
- Digital Logic NOR Gate
- Exclusive-NOR (XNOR) Digital Logic Gate
- Digital Logic NAND Gate – Universal Gate