Series, Parallel & Series-Parallel Connection of Solar Panels
Series, Parallel and Series-Parallel Configuration of Photovoltaic Arrays
What is a Solar Photovoltaic Array?
A Solar Photovoltaic Module is available in a range of 3 WP to 300 WP. But many times, we need power in a range from kW to MW. To achieve such a large power, we need to connect N-number of modules in series and parallel.
A String of PV Modules
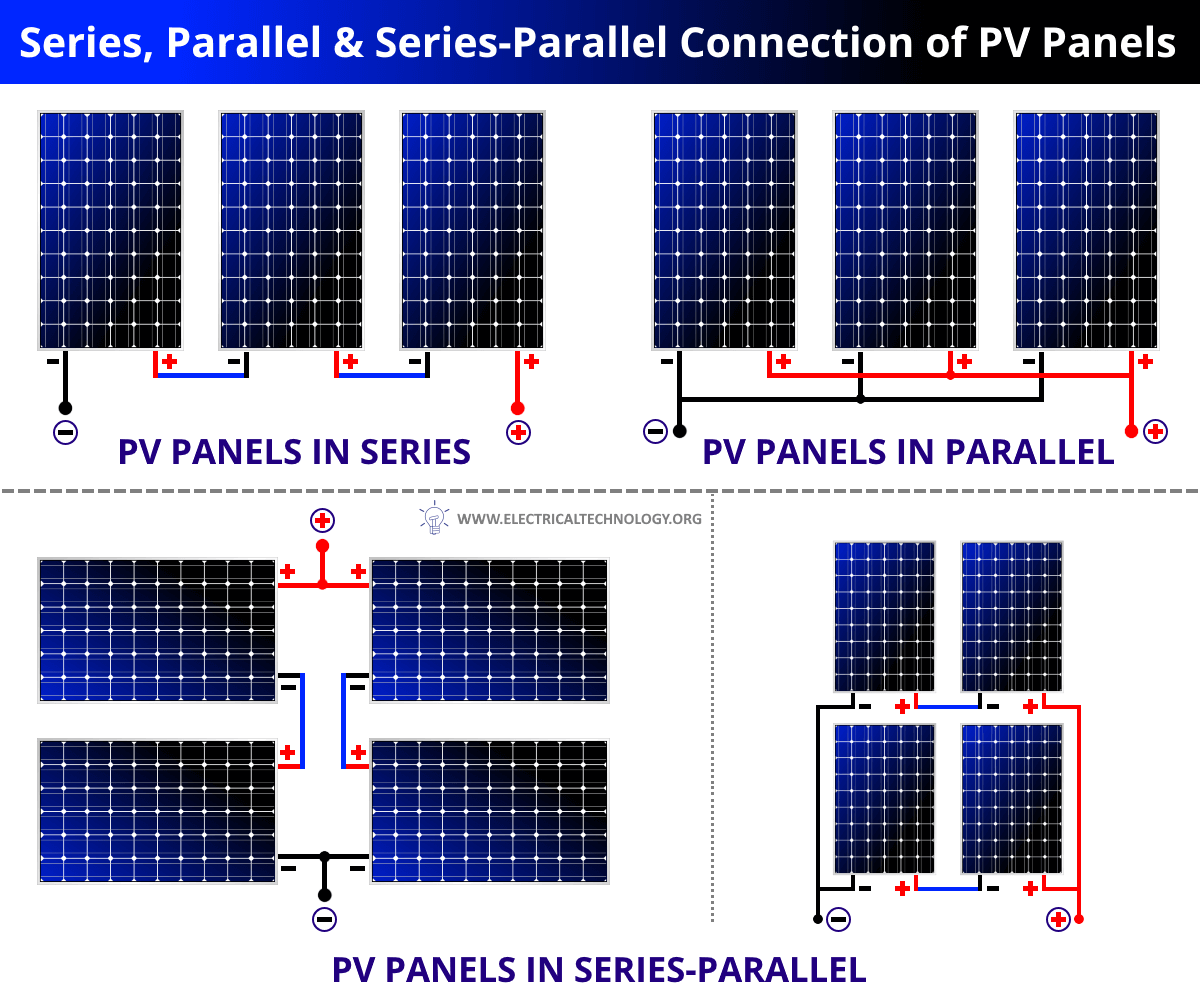
When N-number of PV modules are connected in series. The entire string of series-connected modules is known as the PV module string. The modules are connected in series to increase the voltage in the system. The following figure shows a schematic of series, parallel and series parallel connected PV modules.
PV Module Array
To increase the current N-number of PV modules are connected in parallel. Such a connection of modules in a series and parallel combination is known as “Solar Photovoltaic Array” or “PV Module Array”. A schematic of a solar PV module array connected in series-parallel configuration is shown in figure below.
Solar Module Cell:
The solar cell is a two-terminal device. One is positive (anode) and the other is negative (cathode). A solar cell arrangement is known as solar module or solar panel where solar panel arrangement is known as photovoltaic array.
It is important to note that with the increase in series and parallel connection of modules the power of the modules also gets added.
Related Posts:
- How to Wire Solar Panels in Series-Parallel Configuration?
- Series, Parallel and Series-Parallel Connection of Batteries
Series Connection of Modules
Sometimes the system voltage required for a power plant is much higher than what a single PV module can produce. In such cases, N-number of PV modules is connected in series to deliver the required voltage level. This series connection of the PV modules is similar to that of the connections of N-number of cells in a module to obtain the required voltage level. The following figure shows PV panels connected in series configuration.
With this series connection, not only the voltage but also the power generated by the module also increases. To achieve this the negative terminal of one module is connected to the positive terminal of the other module.
If a module has an open circuit voltage VOC1 of 20 V and other connected in series has VOC2 of 20 V, then the total open circuit of the string is the summation of two voltages
VOC = VOC1 + VOC2
VOC = 20 V + 20 V = 40 V
It is important to note that the summation of voltages at the maximum power point is also applicable in case of PV array.
Calculation of the Number of Modules Required in Series and their Total Power
To calculate the number of PV modules to be connected in series, the required voltage of the PV array should be given. We will also see the total power generated by the PV array. Note that all the modules are identical having the same module parameters.
Step 1: Note the voltage requirement of the PV array
Since we have to connect N-number of modules in series we must know the required voltage from the PV array
- PV array open-circuit voltage VOCA
- PV array voltage at maximum power point VMA
Step 2: Note the parameters of PV module that is to be connected in the series string
PV module parameters like current and voltage at maximum power point and other parameters like VOC, ISC, and PM should also be noted.
Step 3: Calculate the number of modules to be connected in series
To calculate the number of modules “N” the total array voltage is divided by voltage of individual module, Since the PV module is supposed to be working under STC the ratio of array voltage at maximum power point VMA to module voltage at maximum power point VM is taken.
A similar calculation for open-circuit voltage of PV can also be done i.e. ratio of array voltage at open circuit VOCA to module voltage at open circuit VOC. Note that the value of “N” can be a non-integer so we have to take next higher integer and so the value of VMA and VOCA will also increase than what we desired.
Step 4: Calculating the total power of the PV array
The total power of the PV array is the summation of the maximum power of the individual modules connected in series. If PM is the maximum power of a single module and “N” is the number of modules connected in series, then the total power of the PV array PMA is N × PM.
We can also calculate the array power by the product of PV array voltage and current at maximum power point i.e.
VMA × IMA
Related Posts:
- How to Wire Solar Panels & Batteries in Series-Parallel Connection?
- How to Wire Batteries in Series-Parallel to a Solar Panel?
Example:
Now to understand these steps in a more mathematical way. Let’s take an example of a power plant of 2 MW, in which a large number of PV modules are connected in series. The 2 MW inverter can take input voltage from 600 V to 900 V.
Determine the number of modules be connected in series to obtain a maximum power point voltage of 800 V. Also determine the power delivered by this PV array. The parameters of the single PV module are as follows;
- Open circuit voltage VOC = 35 V
- Voltage at maximum power point VM = 29 V
- Short circuit current ISC = 7.2 A
- Current at maximum power point IM = 6.4 A
Step 1: Note the voltage requirement of the PV array
- PV array open-circuit voltage VOCA = Not given
- PV array voltage at maximum power point VMA = 800 V
Step 2: Note the parameters of PV module that is to be connected in the series string
Open circuit voltage VOC = 35 V
Voltage at maximum power point VM = 29 V
Short circuit current ISC = 7.2 A
Current at maximum power point IM = 6.4 A
Maximum Power PM
PM = VM x IM
= 29 V x 6.4 A
PM = 185.6 W
Step 3: Calculate the number of modules to be connected in series
N = VMA / VM
N = 800 / 29
N = 27.58 (Higher integer value 28)
Take higher integer value 28 modules. Due to the higher integer value of N, the value of VMA and VOCA will also increase.
VMA = VM × N
= 29 × 28
= 812 V
Step 4: Calculating the total power of the PV array
PMA = N × PM
= 28 × 185.6
= 5196.8 W
Thus, we need 28 PV modules to be connected in series having a total power of 5196.8 W to obtain the desired maximum PV array voltage of 800 V.
Related Posts:
- How to Wire Solar Panels in Series & Batteries in Parallel?
- How to Wire Solar Panels in Parallel & Batteries in Series?
Mismatch in Series-connected PV Modules
The maximum power in the PV module is the product of voltage and current at maximum power. When the modules are not connected in series then the power produced by an individual module is different. Take the example of table 1 given below.
Table 1
| Modules | VM in Volts | IM in Ampere | PM in Watt |
| Module A | 16 | 4.1 | 65.6 |
| Module B | 15.5 | 4.1 | 63.55 |
| Module C | 15.3 | 4.1 | 62.73 |
| Total | In series = 46.8 | In series = 4.1 | 191.88 |
If the three modules in table 1 are connected in series their voltage is added but the current remains the same considering all the modules are identical having the same value of IM = 4.1 A.
The difference in the voltages of the modules A, B, and C connected in series does not result in the loss of the power produced by the PV module array considering all the modules are identical having the same value of IM = 4.1 A.
But if the current producing capacity of the modules connected in series is not identical then the current flowing through the series-connected PV modules will be equal to the lowest current produced by a module in the string. Take an example table 2 given below.
Table 2
| Modules | VM in Volts | IM in Ampere | PM in Watt |
| Module A | 16 | 4.1 | 65.6 |
| Module B | 15.5 | 3.2 | 49.6 |
| Module C | 15.3 | 4.1 | 62.73 |
| Total | In Series = 46.8 | In Series = 3.2 | 177.93 |
If all the modules in table 2 are connected in series then the current flowing through the series-connected modules is determined by the module with the lowest current. In this case module B has the lowest current of 3.2 A as compared to modules A and C.
So, the current flowing through these three series-connected modules is 3.2 A. Now compare Tables 1 and 2 and the total power produced by both. Due to unidentical current modules in table 2 the total power produced is 177.93 W which is less than the total power produced by modules in table 1 i.e. 191.88 W.
We can see that due to the mismatch in current the output power produced by the series-connected modules is widely affected. So, in the series connection of modules mismatch in voltage is not an issue but mismatch in current results in loss of power. Hence modules with different current ratings should not be connected in series.
Related Posts:
- Introduction to Series, Parallel and Series-Parallel Connections
- Difference Between Series and Parallel Circuit – Comparison
Parallel Connection of Modules
Sometimes to increase the power of the solar PV system, instead of increasing the voltage by connecting modules in series the current is increased by connecting modules in parallel. The current in the parallel combination of the PV modules array is the sum of individual currents of the modules.
The voltage in the parallel combination of the modules remains the same as that of the individual voltage of the module considering that all the modules have identical voltage.
The parallel combination is achieved by connecting the positive terminal of one module to the positive terminal of the next module and negative terminal to the negative terminal of the next module as shown in the following figure. The following figure shows solar panels connected in parallel configuration.
If the current IM1 is the maximum power point current of one module and IM2 is the maximum power point current of other module then the total current of the parallel-connected module will be IM1 + IM2. If we keep on adding modules in parallel the current keeps adding up. It is also applicable for short-circuit current Isc.
Calculation of the Number of Modules Required in Parallel and their Total Power
To calculate the number of PV modules to be connected in parallel, the required current of the PV array should be given. We will also see the total power generated by the PV array. Note that all the modules are identical having the same module parameters.
Step 1: Note the current requirement of the PV array
Since we have to connect N-number of modules in parallel we must know the required current from the PV array
- PV array short-circuit current ISCA
- PV array current at maximum power point IMA
Step 2: Note the parameters of PV module that is to be connected in parallel
PV module parameters like current and voltage at maximum power point and other parameters like VOC, ISC, and PM should also be noted.
Step 3: Calculate the number of modules to be connected in parallel
To calculate the number of modules N the total array current is divided by the current of an individual module, Since the PV module is supposed to be working under STC the ratio of array current at maximum power point IMA to module current at maximum power point IM is taken.
A similar calculation for short-circuit current of PV can also be done i.e. ratio of array short-circuit current ISCA to module short-circuit current ISC.
Note that the value of N can be a non-integer so we have to take next higher integer and so the value of IMA and ISCA will also increase than what we desired.
Step 4: Calculating the total power of the PV array
The total power of the PV array is the summation of the maximum power of the individual modules connected in parallel. If PM is the maximum power of a single module and “N” is the number of modules connected in parallel, then the total power of the PV array PMA is N × PM. we can also calculate the array power by the product of PV array voltage and current at maximum power point i.e. VMA × IMA.
Related Posts:
- Which Bulb Glows Brighter When Connected in Series and Parallel & Why?
- Are The Batteries Connected in Series or Parallel?
Example:
Let’s take an example, calculate the number of modules required in parallel to obtain maximum power point current IMA of 40 A. The system voltage requirement is 14 V. The parameters of the single PV module are as follows;
- Open circuit voltage VOC = 18 V
- Voltage at maximum power point VM = 14 V
- Short circuit current ISC = 6.5 A
- Current at maximum power point IM = 6 A
Step 1: Note the current requirement of the PV array
- PV array short-circuit current ISCA = Not given
- PV array current at maximum power point IMA = 40 A
Step 2: Note the parameters of PV module that is to be connected in parallel
Open circuit voltage VOC = 18 V
Voltage at maximum power point VM = 14 V
Short circuit current ISC = 6.5 A
Current at maximum power point IM = 6 A
Maximum Power:
PM = VM x IM
PM = 14V x 6A
PM = 84 W
Step 3: Calculate the number of modules to be connected in parallel
N = IMA / IM
= 40 / 6
N = 6.66 (Higher integer value 7)
Take higher integer value 7 modules. Due to the higher integer value of N, the value of IMA and ISCA will also increase.
IMA = IM × N
= 6 × 7
IMA = 42 A
Step 4: Calculating the total power of the PV array
PMA = N × PM
= 7 × 84
PMA = 588 W
Thus, we need 7 PV modules to be connected in parallel having a total power of 588 W to obtain the desired maximum PV array current of 40 A.
Mismatch in Parallel-connected PV Modules
In a parallel connection, the issue of mismatch in current is not a problem but the mismatch in voltage is a problem. In parallel-connected modules, the voltage will remain the same if the modules have identical voltage ratings.
But if the voltage rating of parallel-connected modules is different then the system voltage is determined by the module having the lowest voltage rating resulting in the power loss.
The effect of voltage mismatch is not as severe as the current mismatch but care must be taken while choosing the modules. It is recommended that for series combination modules of the same current rating and for parallel combination modules of the same voltage rating should be preferred.
Series – Parallel Connection of Modules – Mixed Combination
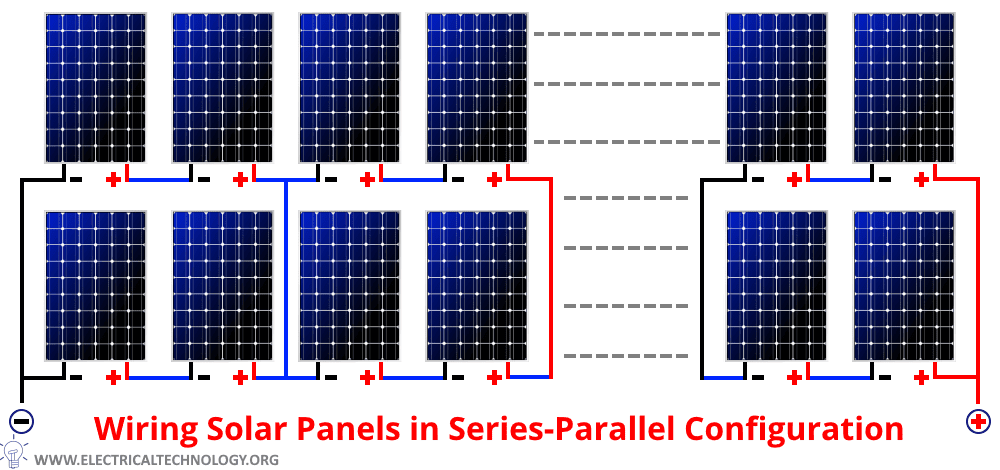
When we need to generate large power in a range of Giga-watts for large PV system plants we need to connect modules in series and parallel. In large PV plants first, the modules are connected in series known as “PV module string” to obtain the required voltage level.
Then many such strings are connected in parallel to obtain the required current level for the system. The following figures shows the connection of modules in series and parallel. To simplify this, take a look at right in the following figure.
Module 1 and module 2 are connected in series let’s call it the string 1. The open-circuit voltage of the string 1 VOC1 is added i.e.
VOC1 = VOC + VOC = 2VOC
Whereas the short-circuit current of string 1 ISC1 is the same i.e.
ISC1 = ISC
Similar to string 1, the modules 3 and 4 make up the string 2. The open-circuit voltage of the string 2 VOC2 is added i.e.
VOC2 = VOC + VOC = 2VOC
Whereas the short-circuit current of string 2 ISC2 is the same i.e.
ISC2 = ISC
Now string 1 and string 2 are connected in parallel, nowhere the voltage remains the same but the current is added i.e. open-circuit voltage of the PV module array
VOCA = VOC1 = VOC2 = 2VOC
And Short circuit current of the PV module array
ISCA = ISC1 + ISC2 = ISC + ISC = 2ISC
The same calculation is applicable for voltage and current at the maximum PowerPoint.
Calculation of the Number of Modules Required in Series – Parallel, and their Total Power
Here for the calculation of the number of modules required in series and parallel, and power we have assumed that all the modules have identical parameters. Note that;
- NS = Number of modules in series
- NP = Number of modules in parallel
Step 1: Note the current, voltage, and power requirement of the PV array
- PV array power PMA
- PV array voltage at maximum power point VMA
- PV array current at maximum power point IMA
Step 2: Note the PV module parameters
PV module parameters like current and voltage at maximum power point and other parameters like VOC, ISC, and PM should also be noted.
Step 3: Calculate the number of modules to be connected in series and parallel
To calculate the number of modules in series Ns the total array voltage is divided by the voltage of an individual module, Since the PV module is supposed to be working under STC the ratio of array voltage at maximum power point VMA to module voltage at maximum power point VM is taken.
Similarly, to calculate the number of modules in parallel Np the total array current is divided by the current of an individual module, Since the PV module is supposed to be working under STC the ratio of array current at maximum power point IMA to module current at maximum power point IM is taken.
Similar calculations for open-circuit voltage and short-circuit current can be done. Note that the value of Ns and NP can be a non-integer so we have to take next higher integer and so the value of IMA, ISCA, VMA, and VOCA will also increase than what we desired.
Step 4: Calculating the total power of the PV array
The total power of the PV array is the summation of the maximum power of the individual modules connected in series and parallel.
If PM is the maximum power of a single module, and NS is the number of modules connected in series and NP is the number of modules connected in parallel, then the total power of the PV array
PMA = NP × NS × PM
We can also calculate the array power by the product of PV array voltage and current at maximum power point i.e.
VMA × IMA
- Related Post: How to Design and Install a Solar PV System?
Example:
Now let’s take an example for the mix – combination. We have to determine the number of modules required for a PV array having the following parameters;
- Array power PMA = 40 KW
- Voltage at maximum power point of array VMA = 400 V
- Current at maximum power point of array IMA = 100 A
- The module for the design of the array has the following parameters;
- Voltage at maximum power point of module VM = 70 V
- Current at maximum power point of module IM =17 A
Step 1: Note the current, voltage, and power requirement of the PV array
- PV array power PMA = 40 KW
- PV array voltage at maximum power point VMA = 400 V
- PV array current at maximum power point IMA = 100 A
Step 2: Note the PV module parameters
Voltage at maximum power point of module VM = 70 V
Current at maximum power point of module IM = 17 A
Maximum power PM:
PM = VM x IM
PM = 70V x 17A
PM = 1190 W
Step 3: Calculate the number of modules to be connected in series and parallel
NS = VMA / VM
NS = 400 / 70
NS = 5.71 (Higher integer value 6)
Take higher integer value 6 modules. Due to the higher integer value of NS, the value of VMA and VOCA will also increase.
VMA = VM × NS
= 70 × 6
VMA = 420 V
Now,
NP = IMA / IM
NP = 100 / 17
NP = 5.88 (Higher integer value 6)
Take higher integer value 6 modules. Due to the higher integer value of NP, the value of IMA and ISCA will also increase.
IMA = IM × NP
IMA = 17 × 6
IMA = 102 A
Step 4: Calculating the total power of the PV array
PMA = NS × NP × PM
= 6 × 6 × 1190
PMA = 42840 W
Thus, we need 36 PV modules. A string of six modules connected in series and six such strings connected in parallel, having a total power of 42840 W to obtain the desired maximum PV array current of 100 A and voltage of 400 V.
Note that due to higher integer value of 6 the maximum PV array current and voltage is 102 A and 420 V respectively.
Conclusion
In this article, an in-depth study of the solar photovoltaic module and array was carried out. The need, structure, and design of the modules for higher power level was studied. It also included a procedure for parameter measurement and explanation of bypass diode and blocking diode for the safety of the module.
We also saw an explanation of the PV module array along with its need and connection combination. Calculation and procedure for the design of series, parallel, and mix connections were done in detail along with the study of mismatch in voltage and current of the modules. Such a study of Photovoltaic module and array is a must requirement for a designer of the PV system.
The article gives a significant design understanding of important components (modules and array) in the PV system, which can be utilized to make a proper, efficient, and reliable design in a PV system.
Related Posts:
- Basic Components Needed for Solar Panel System Installation
- A Complete Guide About Solar Panel Installation. Step by Step Procedure with Examples
- How to Make a Simple Solar Cell? Working of Photovoltaic Cells
- How to Wire Batteries in Parallel to a Solar Panel and UPS?
- How to Wire Batteries in Series to a Solar Panel and UPS?
- How to Wire Solar Panel to 12V DC Load and Battery?
- How to Wire Solar Panel to 120-230V AC Load and Inverter?
- How to Wire Solar Panel & Batteries in Parallel?
- How to Wire Solar Panel & Batteries in Series?








Dear Sir, I have 8 solar panel each 180 watt, and UPS 1000 watt, please guide me how many solar panel can be attach with this UPS? Regards, Asghar
I kind of disagree with your calculation of total power of PV arrays in series.1/Pt=1/P1 + 1/P2 + … + 1/Pn
Hence when devices are connected in series, power stays constant across all devices
Thank you for providing the step by step solar panel wiring guide.
Great explanation of series, parallel, and series-parallel connections for solar panels! Proper wiring is crucial, but maintenance is equally important for keeping panels efficient.
I am student, studying solar installation i need lectures from this website.
I am from Sierra leone 🇸🇱 West Africa