Corona Effect and Discharge in Power Transmission Lines
Corona Effect or Corona Discharge in Power Transmission Lines
What is Corona Effect or Corona Discharge?
When a low alternating potential difference is applied across two conductors with spacing significantly larger than their diameters, there is no apparent change in the atmospheric air condition around the wires.
However, when the applied voltage exceeds a certain value, called the critical disruptive voltage, the conductors are surrounded by a faint violet glow called corona.
The phenomenon of corona is accompanied by a hissing sound, production of ozone, power loss and radio interference.
The higher the voltage is raised, the larger and higher the luminous envelope becomes, and greater are the sound, the power loss and the radio noise. If the applied voltage is increased to breakdown value, a flash-over will occur between the conductors due to the breakdown of air insulation.
Corona effect or corona discharge in transmission lines and power system may be defined as:
The phenomenon of violet glow, hissing noise and production of ozone gas in an overhead transmission line is known as corona.
If the conductors are polished and smooth, the corona glow will be uniform throughout the length of the conductors, otherwise the rough points will appear brighter. With DC voltage, there is difference in the appearance of the two wires. The positive wire has uniform glow about it, while the negative conductor has spotty glow.
- Related Post: What is Sag in Overhead Power Transmission Lines?
Difference Between Corona Effect and Skin Effect
The differences between Corona and skin effect are as follows.
Corona Effect / Discharge:
As described above, corona is an effect of violet glow, hissing noise and production of ozone gas in an overhead transmission line is known as corona which leads to hissing sound, production of ozone, power loss and radio interference in power system.
Skin Effect:
Skin effect is a behavior or tendency of alternating current to flow through the surface (outer layer) of a conductor instead of the core of the wire in power system transmission lines.
In this scenario, the current density is lager near the surface of the wire or conductor and decreases with greater depths in the conductor which leads to increase in resistance of the conductor, thus increase the overall power loss in the power system (generally transmission lines).
Theory of Corona Formation
Some ionization is always present in air due to cosmic rays, ultra-violet radiations and radioactivity. Therefore, under normal conditions, the air around the conductors contains some ionized particles (i.e., free electrons and +ve ions) and neutral molecules.

When p.d.is applied between the conductors, potential gradient is set up in the air which will have maximum value at the conductor surfaces. Under the influence of potential gradient, the existing free electrons acquire greater velocities. The greater the applied voltage, the greater the potential gradient and more is the velocity of free electrons.
When the potential gradient at the conductor surface reaches about 30kV per cm (max. value), the velocity acquired by the free electrons is sufficient to strike a neutral molecule with enough force to dislodge one or more electrons from it.
This produces another ion and one or more free electrons, which is turn are accelerated until they collide with other neutral molecules, thus producing other ions. Thus, the process of ionization is cumulative. The result of this ionization is that either corona is formed or spark takes place between the conductors.
- Related Post: Ferranti Effect – Causes, Advantages & Disadvantages
Mathematical Modelling of Corona Effect
Corona effect or corona discharge is a phenomenon that results from a partial discharge in the air (or in any fluid) caused by the ionization of the environment when an electrical current flows in a conductor and when the electric field gradient[1] is strong enough to ionize the environment, but it is not strong enough to cause dielectric breakdown[2] or arcing between the conductors.
This phenomenon that is characterized by a glow (mostly with a color in blue/violet spectrum), mainly happens in overhead lines, close to the suspension and strain insulators, when the distance between conductors is much greater than the diameters of the conductors.
Generally for parallel conductors in the air there is corona effect when.
D/r < 5.85
Where:
- r is the radius of the conductors
- D is the distance between the conductors
When studying corona effect, it is important to evaluate the minimum value of the voltage between phases or between one phase and the neutral (or the ground) for which the corona effect takes place.
This voltage is named Critical Disruptive Voltage. If r [cm] is the radius of the conductor, d [cm] is the distance between the conductor and the neutral (or the ground) and U [V] is the gradient of the electric field E (mathematical notation: grad E), the critical disruptive voltage that we will designated as G, is calculated by the equation:
G = (U / (r x ln (d/r)) [V/m]
Where ln represents the natural logarithm.
To corona effect takes place it is necessary that G will be equal or greater than the disruption voltage of the air, that at atmospheric pressure (1.01325×105 Pa = 1 atm = 760 mmHg[3]) and at a temperature of 25 ºC is equal to 30 kV/cm – considering the maximum value of U – or 21.2 kV/cm – considering the rms[4] value of U.
Designating by G0 the value of grad E that obeys to the above condition the critical value of the disruption voltage (UC) is calculated by the equation:
UC = G0 x r x ln (d/r) [kV/phase]
For different conditions of temperature and of atmospheric pressure, the density of the air is also different; it is possible to express that variation by a factor δ that for a given pressure P [Pa] and temperature θ [ºC] is calculated by the equation:
δ = (3.92 × 1.01325×105 × P) / ((273 + θ) × 760)
Being G’0 the value of grad E corresponding to the new atmospheric conditions, its value is calculated by the equation:
G’0 = δ × G0
Hence, the critical value of the disruption voltage (U’C) is calculated by the equation:
U’C = G0 × r x δ x ln (d/r) [kV/phase]
Taking into account the irregularity of the conductor surface and expressing that irregularity as a factor m0, the value of U’C is then:
U’C = m0 × G0 x r x δ x ln (d/r) [kV/phase]
Common values of m0 are:
- Polished conductors: m0 = 1
- Dirty conductors: m0 = 0.92-0.98
- Stranded conductors: m0 = 0.8-0.87
Another value used to characterize the corona effect is the Visual Critical Voltage, represented by UV, that is the minimum voltage between one phase and the neutral (or the ground) for which the corona effect takes place all along the conductor. That voltage is calculated by the following empirical equation:
UV = mv x G0 x δ x 3 × (1 + (0.3 / √(δ x r)) x ln (d/r) [kV/phase]
Factor mv is also a “measure” of the irregularity of the conductor, assuming the following values.
- Polished conductors: mv = 1
- Rough conductors: mv = 0.72-0.82
Another value that must be calculated when studying the corona effect is the losses caused by this effect; considering the rms value of UC and being U the rms rated voltage of the network, both in kV, and f [Hz] the rated network frequency, losses by corona effect (PCO) are calculated by the equation:
PCO = 242.2 x ((f + 25) / δ) × √(r/d) x (U(exp)2 – Uc2) x 10-5 [kW/km/phase]
Important Terms Related to Corona
The phenomenon of corona plays an important role in the design of an overhead transmission line. Therefore, it is profitable to consider the following terms much used in the analysis of corona effects:
Critical Disruptive Voltage
It is the minimum phase-neutral voltage at which corona occurs. Consider two conductors of radius r (cm) and spaced d (cm) apart. If V is the phase-neutral potential, then potential gradient at the conductor surface is given by:
In order that corona is formed, the value of g must be made equal to the breakdown strength of air. The breakdown strength of air at 76 cm pressure and temperature of 25ºC is 30 kV/cm (max) or 21·2 kV/cm (r.m.s.) and is denoted by go.
If VC is the phase-neutral potential required under these conditions, then,
where go = breakdown strength of air at 76 cm of mercury and 25ºC = 30 kV/cm (max) or 21·2 kV/cm (r.m.s.)
- ∴ Critical disruptive voltage, Vc = go r loge d/r
The above expression for disruptive voltage is under standard conditions i.e., at 76 cm of Hg and 25ºC. However, if these conditions vary, the air density also changes, thus altering the value of go.
The value of go is directly proportional to air density. Thus the breakdown strength of air at a barometric pressure of b (cm) of mercury and temperature of tºC becomes δ go where
δ = air density factor = 3.92b / 273 + t
Under standard conditions, the value of δ = 1.
- ∴ Critical disruptive voltage ,Vc = go δ r loge d/r
Correction must also be made for the surface condition of the conductor. This is accounted for by multiplying the above expression by irregularity factor mo.
- ∴ Critical disruptive voltage, Vc = mo go δ r loge d/r …. kV/phase
- mo = 1 for polished conductors
- = 0·98 to 0·92 for dirty conductors
- = 0·87 to 0·8 for stranded conductors
Visual Critical Voltage
It is the minimum phase-neutral voltage at which corona glow appears all along the line conductors.
It has been seen that in case of parallel conductors, the corona glow does not begin at the disruptive voltage Vc but at a higher voltage Vv , called visual critical voltage.
The phase-neutral effective value of visual critical voltage is given by the following empirical formula :
where mv is another irregularity factor having a value of 1·0 for polished conductors and 0·72 to 0·82 for rough conductors.
- Related Post: Power Distribution in Industries
Factors & Conditions Effecting Corona
The phenomenon of corona is affected by the physical state of the atmosphere as well as by the conditions of the line. The following are the factors upon which corona depends :
Atmosphere
As corona is formed due to ionization of air surrounding the conductors, there-fore, it is affected by the physical state of atmosphere. In the stormy weather, the number of ions is more than normal and as such corona occurs at much less voltage as compared with fair weather.
Conductor size
The corona effect depends upon the shape and conditions of the conductors. The rough and irregular surface will give rise to more corona because unevenness of the surface decreases the value of breakdown voltage. Thus a stranded conductor has irregular surface and hence gives rise to more corona that a solid conductor.
Spacing Between Conductors
If the spacing between the conductors is made very large as compared to their diameters, there may not be any corona effect. It is because larger distance between conductors reduces the electrostatic stresses at the conductor surface, thus avoiding corona formation.
Line Voltage
The line voltage greatly affects corona. If it is low, there is no change in the condition of air surrounding the conductors and hence no corona is formed. However, if the line voltage has such a value that electrostatic stresses developed at the conductor surface make the air around the conductor conducting, then corona is formed.

Power Loss Due to Corona
Formation of corona is always accompanied by energy loss which is dissipated in the form of light, heat, sound and chemical action. When disruptive voltage is exceeded, the power loss due to corona is given by:
Methods of Reducing Corona Discharge
It has been seen that intense corona effects are observed at a working voltage of 33 kV or above. Therefore, careful design should be made to avoid corona on the sub-stations or bus-bars rated for 33kV and higher voltages otherwise highly ionized air may cause flash-over in the insulators or between the phases, causing considerable damage to the equipment.
The corona effects can be reduced by the following methods:
By Increasing Conductor Size
By increasing conductor size, the voltage at which corona occurs is raised and hence corona effects are considerably reduced. This is one of the reasons that ACSR conductors which have a larger cross-sectional area are used in transmission lines.
By Increasing Conductor Spacing.
By increasing the spacing between conductors, the voltage at which corona occurs is raised and hence corona effects can be eliminated. However, spacing cannot be increased too much otherwise the cost of supporting structure (e.g., bigger cross arms and supports) may increase to a considerable extent.
- Related Post: Types of Faults in Electrical Power System
Calculations of Corona Discharge – Solved Examples
Advantages and Disadvantages of Corona Effect
Corona effects on communication lines. Corona has many advantages and disadvantages. In the correct design of a high voltage overhead line, a balance should be struck between the advantages and disadvantages. Below are the Advantages and disadvantages of Corona.
Advantages
- Due to corona formation, the air surrounding the conductor becomes conducting and hence virtual diameter of the conductor is increased. The increased diameter reduces the electrostatic stresses between the conductors.
- Corona reduces the effects of transients produced by surges.
Disadvantages
- Corona is accompanied by a loss of energy. This affects the transmission efficiency of the line.
- Ozone is produced by corona and may cause corrosion of the conductor due to chemical action.
- The current drawn by the line due to corona is non-sinusoidal and hence non-sinusoidal voltage drop occurs in the line. This may cause inductive interference with neighboring Communication lines.
[1]Gradient is a differential operator that when applied to a scalar field F defines the vector in which direction is achieved the greatest rate of increase of that field. [2]Dielectric breakdown of an insulating material happens when the value of the electric field applied to that material is too high, causing the material to become conductive. In the air this breakdown happens when the value of the electric field is ≈ 3×106 V/m. In this case a disruption takes place. [3] Between brackets are indicated pressure units: Pa – Pascal; atm – atmosphere; mmHg – millimeter of mercury. [4]RMS: Root Mean Square, a measure of the magnitude of a varying quantity.
Related Posts:
- Overhead Lines Protection – Faults and Protection Devices
- Design and Installation of EHV/EHV and EHV/HV Substations
- Power Factor Improvement Methods with their Advantages & Disadvantages
- HV And MV Switch Disconnectors And Isolators in Power System
- Power System Restoration & Outage, Voltage Collapse & Switching Programs
- Comparison between AC and DC Transmission System
- What are the Effects of Temperature on Sag in Overhead Lines?
- Why are Overhead Power Lines Loose on Electric Poles & Towers?
- Classification of Electric Power Distribution Network Systems
- Types of HVDC Systems and MTDC Configurations
- Differences Between HVAC and HVDC – Power Transmission
- Treeing in XLPE Insulated Medium & High Voltage Cables


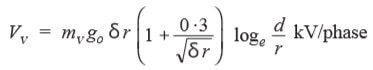
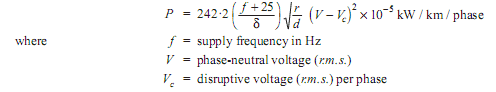

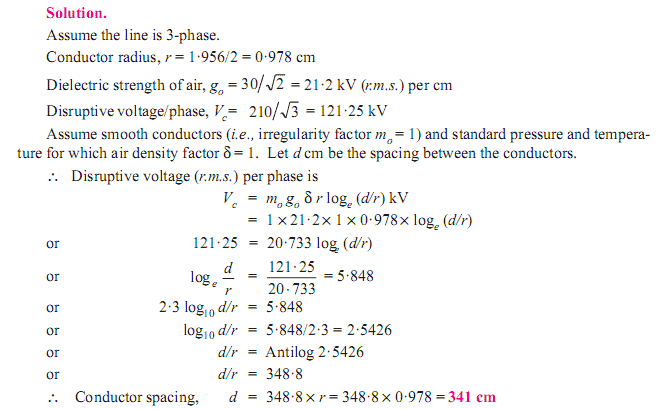








Nice n informative articles