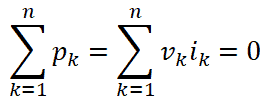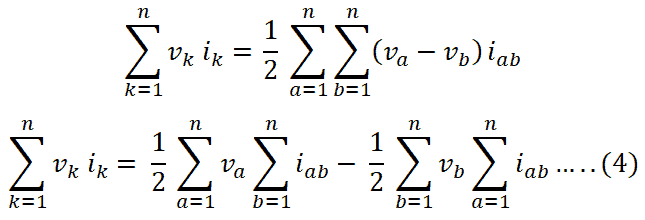Tellegen’s Theorem – Solved Examples & MATLAB Simulation

Tellegen’s Theorem – Step by Step Guide with Solved Examples

What is Tellegen’s Theorem?

Tellegen’s theorem was published by a Dutch electrical engineer and inventor Bernard D.H. Tellegen in 1952. This theorem is the most important and fundamental theorem among other theorems in network analysis. Most other theorems are derived from this theorem.

Tellegen’s theorem depends on Kirchhoff’s law. Therefore, this theorem can apply to the network which obeys Kirchhoff’s law. This theorem can be applied to the wide range of the network having linear or nonlinear, time-variant or non-variant, passive or active elements.

Tellegen’s theorem states that;

“The summation of instantaneous power consumed by various elements in various branches is equal to zero for any network.”

Tellegen’s theorem works based on the principle of the law of conservation of energy. This theorem is used in chemical and biological applications to find the dynamic behavior of the physical network. In signal processing, this theorem is used to design filters.

• Related Post: Thevenin’s Theorem. Step by Step Guide with Solved Example

Mathematical Equation

For a general analysis of the theorem, we consider the ‘n’ number of elements are given in the network. The instantaneous current passes through the element is i₁, i₂, i₃, …., i_n. And the instantaneous voltage of this branch is v₁, v₂, v₃, …., v_n.

Therefore, the instantaneous current and voltage of element-1 are i₁ and v₁. The instantaneous power (p₁) consumed by this element is v₁i₁.

p₁ = v₁ i₁

Instantaneous power of element-2 is (p₂);

p₂ = v₂ i₂

Similarly, the instantaneous power of n^th element is (p_n);

p_n = v_n i_n

According to Tellegen’s theorem, the summation of all instantaneous power is zero. It means we need to sum all instantaneous power p₁, p₂, p₃, …., p_n.

p₁ + p₂ + p₃ + … + p_n = 0

v₁ i₁+ v₂ i₂ + v₃ i₃ + … + v_n i_n = 0

In general form, we can write the above equation for the k^th branch;

Where,

• n = total number of branches in the network
• v_k = instantaneous voltage of k^th branch
• i_k = instantaneous current of k^th branch
• p_k = instantaneous power of k^th branch

Now, consider the below figure as branch AB is equal to branch k.

Therefore, instantaneous voltage v_k;

v_k = v_a – v_b

And the instantaneous current passing through the branch (a to b) is i_k;

i_k = i_ab

So, the instantaneous power p_k is;

p_k = v_k i_k = (v_a – v_b) i_ab ….. (1)

Now, we consider the opposite direction of instantaneous current (b to a);

i_ab = – i_ab

Instantaneous voltage;

v_k = v_b – v_a

The instantaneous power p_k is;

p_k = v_k i_k = (v_b – v_a) i_ba ….. (2)

Summing of equation-1 and 2;

2v_k i_k = (v_a – v_b) i_ab + (v_b – v_a) i_ba

v_k i_k = 1/2 [(v_a – v_b) i_ab + (v_b – v_a) i_ba] ….. (3)

This equation can be written as below for n-branches;

According to Kirchhoff’s current law, the algebraic summation of current is zero at a node of the circuit.

Hence,

If we put this value in the equation-4, we obtain;

Thus, it is proved that the summation of power delivered to the network is zero. Therefore, it’s proved Tellegen’s theorem. It is also described that the sum of power absorbed by the elements of the network is equal to the sum of power delivered by the sources.

• Related Post: Norton’s Theorem. Step by Step Guide with Solved Example

Steps to Follow for Tellegen’s Theorem

We need to follow the below steps to solve any electrical network by Tellegen’s theorem.

Step-1: We need to find a number of branches in the given electrical network. Then find the power dissipate across each branch. To find power, we need to find the voltage or current of that branch using any conventional analysis method.

Step-2: Find the instantaneous power of each branch.

Step-3: The branch that has an energy source that is considered as a power delivering branch. And the branch has other elements is considered as a power absorbing branch. Now identify the power delivering branch and power absorbing branch.

Step-4: Assume positive sign in power delivering branch and negative voltage drop in power absorbing branch. You can assume reverse signs also. But cannot change throughout the example.

Step-5: To justify Tellegen’s theorem, we need to add all power calculated from all branches. And this summation always is zero.

• Related Post: SUPERMESH Circuit Analysis – Step by Step with Solved Example

Let’s understand with an example.

Tellegen’s Theorem Solved Example

Example #1

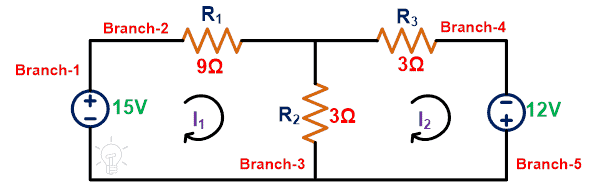
Justify Tellegen’s theorem for the below network.

Solution:

Step-1: The given circuit network has 5 branches. To calculate instantaneous power, we need to find the current passes through each branch. For that, we will apply KVL to the network.

Apply KVL to the loop-1;

15 = 12I₁ – 3I₂

Apply KVL to the loop-2;

12 = – 3I₂ + 6I₂

By solving the above equations, we can find the values of loop current I₁ and I₂. And these values are;

I₁ = 2A

I₂ = 3A

Step-2: Current passing through the branch-3 is;

I₁₂ = I₂ – I₁ = 3 – 2 = 1A

We have current flowing through all branches. Now, find the power of each branch.

P₁ = V I₁ = 15 x 2 = 30W

P₂ = R₁ I₁² = 9 x 4 = 36W

P₃ = R₁ I₁₂² = 3 x 1 = 3W

P₄ = R₃ I₂² = 3 x 9 = 27W

P₅ = V I₂ = 12 x 3 = 36W

Step-3: There are two branches having sources. These branches are power delivering branches and the other three branches are power absorbing branches.

Here, for this example, we assume that the sign of the power delivering branch is positive and the sign of the power absorbing branch is negative. Therefore, branch-1 and 5 are power delivering branches and other branches are power absorbing branches.

Step-4: The sign of power P₁ and P₅ is positive (power delivering branches) and the sign of P₂, P₃, and P₄ is negative (power absorbing branches).

Step-5: Now, we need to find a summation of power dissipated by all branches.

P₁ – P₂ – P₃ – P₄ + P₅ = 30W – 36W – 3W – 27W + 36W = 0W

So, the summation of instantaneous power is zero. And hence, this theorem is proved.

• Related Post: SUPERNODE Circuit Analysis – Step by Step with Solved Example

Example #2

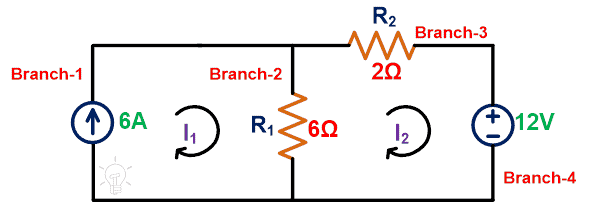
Find the voltage across 6A current source using Tellegen’s theorem.

Solution:

Step-1: We need to calculate voltage or current passes through the element. For that, we apply KCL or KVL to the given network.

Apply KVL to the loop-2;

-12 = 8I₂ – 6I₁

Current passes through the branch having current source are I₁;

I₁ = 6A

Put this value in the above equation;

-12 = 8I₂ – 6(6)

-12 = 8I₂ – 36

36 – 12 = 8I₂

24 = 8I₂

I₂ = 3A

Step-2: Current passes through the branch-2 is;

I₁₂ = I₁ – I₂ = 6 – 3 = 3A

Now, find the power of each branch;

P₁ = V I₁ = V x 6 = 6 x V

P₂ = R₁ I₁₂² = 6 x 9 = 54W

P₄ = R₂ I₂² = 2 x 9 = 18W

P₄ = V I₂ = -12 x 3 = -36W

Step-3: Here, two branches having energy sources. Therefore, we have to consider these branches as power delivering branches. And set the positive sign to the instantaneous power.

The other two branches having resistors only. So, these branches are power absorbing branches and set the negative sign to the instantaneous power.

Step-4: Power P₁ and P₄ have a positive sign and power P₂ and P3 have a negative sign.

Step-5: Now, we need to sum up all instantaneous power.

P₁ – P₂ – P₃ + P₄ = 0W

P₁ – 54 – 18 + 36 = 108W

The power delivered by the 6A current source is 108W. Therefore, the voltage across the current source is calculated by;

P₁ = V I

108W = V x 6A

V = 18V

Therefore, the voltage across the current source is 18V.

• Related Post: Maximum Power Transfer Theorem for AC & DC Circuits

Analyzing & Simulation of Tellegen’s Theorem Using MATLAB  

Aim:

Prove Tellegen Theorem for the circuit diagram given in the above example.

Requirement: MATLAB

Theory:

According to Tellegen’s theorem, the summation instantaneous power of all branches is equal to zero. To prove this theorem, we need to calculate the instantaneous power of all branches.

To find the instantaneous power, we need to calculate the voltage or current of all branches. For that, we can use KCL or KVL theorems. But here we will use the MATLAB Simulink model to find the current and voltage.

We can use other software also like multisim, psim, etc. We will construct a circuit diagram in the Simulink model. By the Simulink model, you can find the voltage and current of each branch.

After that, you can find the instantaneous power from the voltage and current. You can directly find the instantaneous power from some software. 

MATLAB Simulink Model

The below figure shows the circuit diagram of the above example.

Click image to enlarge

In this figure, we can directly find the voltage and current from the display. You can compare these values by calculating the voltage and current with the help of KCL or KVL.

Calculation

After calculating voltage or current, you can find the instantaneous power. Or you can directly find the instantaneous power from the software. All we need is instantaneous power. And after that, we need to add all powers.

The summation of power is always zero. For this example, we compare the value of voltage and current found from the Simulink and the same values calculated in the previous example using KVL and KCL. These values are the same.

These values are also calculated by the connecting resistors and sources on the breadboard. And we can measure the voltage and current passes through all branches with the help of a voltmeter and ammeter.

Therefore, it is proved Tellegen’s theorem.

• Related Post: Kirchhoff’s Current & Voltage Law (KCL & KVL) | Solved Example

Application of Tellegen’s Theorem

This theorem is very fundamental and widely used in circuit analysis. There are many applications of this theorem. Some applications are listed below.

• For designing the filters, this theorem is very useful in the applications of digital signal processing.
• To determine the stability of chemical plants, this theorem is used in chemical engineering.
• This theorem applies to the lumped system having linear-nonlinear, active-passive, time-variant/time-invariant elements.
• This theorem is used in the biological process.
• It is used in topology and analysis of structure reaction.
• It is also used to find the dynamic behavior of the physical network.

Related Electric Circuit Analysis Tutorials:

• Superposition Theorem – Circuit Analysis with Solved Example
• Cramer’s Rule Calculator – 2 and 3 Equations System for Electric Circuits
• Wheatstone Bridge – Circuit, Working, Derivation and Applications
• Electrical and Electronics Engineering Calculators
• 5000+ Electrical and Electronic Engineering Formulas & Equations