What is a PID Controller? Its Types, Working and Applications
PID Controllers – What are they and How Do they Work?
The PID controller is the most common control algorithm used in industrial automation and applications, with more than 95% of industrial controllers being of the PID type. These controllers are employed for achieving more precise and accurate control of various parameters.
Most often, PID controllers are used for the regulation of temperature, pressure, speed, flow, and other process variables. Due to their robust performance and functional simplicity, they have been widely accepted in numerous industrial applications where precise control is a primary requirement. Let’s now explore how the PID controller works.
- Related Post: What is Distributed Control System (DCS)?
What is a PID Controller?
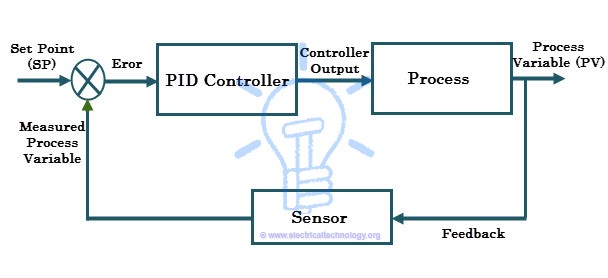
A PID controller, which stands for Proportional-Integral-Derivative controller, is a feedback control system commonly used in industrial automation and process control. It is a combination of proportional, integral, and derivative actions which is more commonly referred to as PID action, hence the name PID (Proportional-Integral-Derivative) controller. These three basic coefficients are adjusted in each PID controller for a specific application to achieve an optimal response.
It gets the input parameter from the sensor which is referred as actual process variable. It also accepts the desired actuator output, which is referred as set variable, and then it calculates and combines the proportional, integral and derivative responses to compute the output for the actuator.
Consider the typical control system shown in above figure in which the process variable of a process has to be maintained at a particular level. Assume that the process variable is temperature (in centigrade). In order to measure the process variable (i.e., temperature), a sensor is used (let us say an RTD).
A set point is the desired response of the process. Suppose the process has to be maintained at 80 degree centigrade, and then the set point is 80 degree centigrade. Assume that the measured temperature from the sensor is 50 degree centigrade, (which is nothing but a process variable) but the temperature set point is 80 degree centigrade.
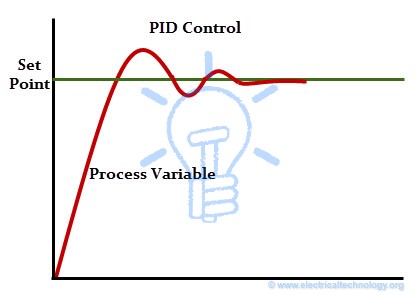
This deviation of actual value from the desired value in the PID control algorithm causes to produce the output to the actuator (here it is a heater) depending on the combination of proportional, integral and derivative responses. So the PID controller continuously varies the output to the actuator till the process variable settle down to the set value. This is also called as closed loop feedback control system.
Related Post:
- What is AC Drive? Working & Types of Electrical Drives & VFD
- What is DC Drive? Operation and Classification of DC Drives
Working of PID Controller
In manual control, the operator may periodically read the process variable (that has to be controlled such as temperature, flow, speed, etc.) and adjust the control variable (which is to be manipulated in order to bring control variable to prescribed limits such as a heating element, flow valves, motor input, etc.). On the other hand, in automatic control, measurement and adjustment are made automatically on a continuous basis.
All modern industrial controllers are of automatic type (or closed loop controllers), which are usually made to produce one or combination of control actions. These control actions include
- ON-OFF Controller
- Proportional Controller
- Proportional-Integral Controller
- Proportional-Derivative Controller
- Proportional-Integral-Derivative Controller
In case of ON-OFF controller, two states are possible to control the manipulated variable, i.e., either fully ON (when process variable is below the set point) or Fully OFF (when process variable is above the set point). So the output will be of oscillating in nature. In order to achieve the precise control, most industries use the PID controller (or PI or PD depends on the application). Let us look at these control actions.
Related Posts:
- SCADA Systems for Electrical Distribution
- Programmable Logic Controllers (PLC) for Industrial Control
P-Controller
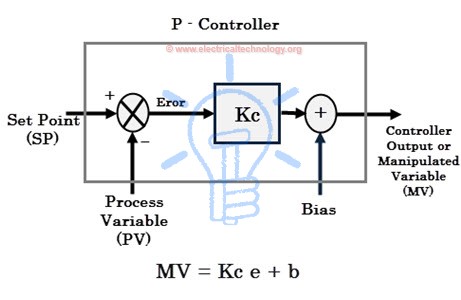
Proportional control or simply P-controller produces the control output proportional to the current error. Here the error is the difference between the set point and process variable (i.e., e = SP – PV). This error value multiplied by the proportional gain (Kc) determines the output response, or in other words proportional gain decides the ratio of proportional output response to error value.
For example, the magnitude of the error is 20 and Kc is 4 then proportional response will be 80. If the error value is zero, controller output or response will be zero. The speed of the response (transient response) is increased by increasing the value of proportional gain Kc. However, if Kc is increased beyond the normal range, process variable starts oscillating at a higher rate and it will cause instability of the system.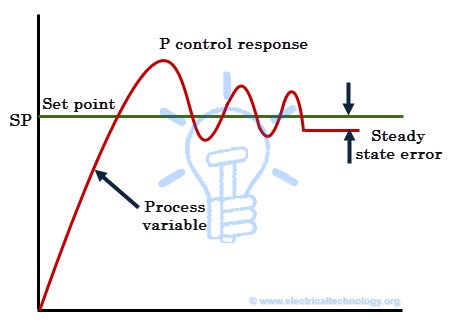
Related Posts:
- What is Industrial Automation | Types of Industrial Automation
- Smart Home Automation System – Circuit and Source Code
I-Controller
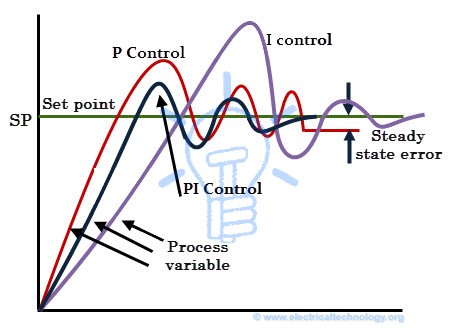
- Integral controller or I-controller is mainly used to reduce the steady state error of the system. The integral component integrates the error term over a period of time until the error becomes zero. This results that even a small error value will cause to produce high integral response. At the zero error condition, it holds the output to the final control device at its last value in order to maintain zero steady state error, but in case of P-controller, output is zero when the error is zero.
If the error is negative, the integral response or output will be decreased. The speed of response is slow (means respond slowly) when I-controller alone used, but improves the steady state response. By decreasing the integral gain Ki, the speed of the response is increased.
For many applications, proportional and integral controls are combined to achieve good speed of response (in case of P controller) and better steady state response (in case of I controller). Most often PI controllers are used in industrial operation in order to improve transient as well as steady state responses. The responses of only I-control, only p-control and PI control are shown in below figure.
Related Posts:
- What is a Sensor? Different Types of Sensors with Applications
- What is a Transducer? Types of Transducers and Applications
D- Controller Response
A derivative controller (or simply D-Controller) sees how fast process variable changes per unit of time and produce the output proportional to the rate of change. The derivative output is equal to the rate of change of error multiplied by a derivative constant. The D-controller is used when the processor variable starts to change at a high rate of speed.
In such case, D-controller moves the final control device (such as control valves or motor) in such direction as to counteract the rapid change of a process variable. It is to be noted that D-controller alone cannot be used for any control applications.
The derivative action increases the speed of the response because it gives a kick start for the output, thus anticipates the future behavior of the error. The more rapidly D-controller responds to the changes in the process variable, if the derivative term is large (which is achieved by increasing the derivative constant or time Td).
In most of the PID controllers, D-control response depends only on process variable, rather than error. This avoids spikes in the output (or sudden increase of output) in case of sudden set point change by the operator. And also most control systems use less derivative time td, as the derivative response is very sensitive to the noise in the process variable which leads to produce extremely high output even for a small amount of noise.
Therefore, by combining proportional, integral, and derivative control responses, a PID controller is formed. A PID controller finds universal application; however, one must know the PID settings and tune it properly to produce the desired output. Tuning means the process of getting an ideal response from the PID controller by setting optimal gains of proportional, integral and derivative parameters.
There are different methods of tuning the PID controller so as to get desired response. Some of these methods include trial and error, process reaction curve technique and Zeigler-Nichols method. Most popularly Zeigler-Nichols and trial and error methods are used.
This is about the PID controller and its working. Due to the simplicity of controller structure, PID controllers are applicable for a variety of processes. And also it can be tuned for any process, even without knowing detailed mathematical model of process. Some of the applications include, PID controller based motor speed control, temperature control, pressure control, flow control, level of the liquid, etc.
Related Posts:
- Difference Between Soft Starter & VFD (Variable Frequency Drive)
- What is a VFD (Variable Frequency Drive)? – Circuit, Working, Types & Applications
Real-Time PID Controllers
There are different types PID controllers available in today’s market, which can be used for all industrial control needs such as level, flow, temperature and pressure. When deciding on controlling such parameters for a process using PID, options include use either PLC or standalone PID controller.
Standalone PID controllers are used where one or two loops are needed to be monitored and controlled or in the situations where it difficult to access with larger systems. These dedicated control devices offer a variety of options for single and dual loop control. Standalone PID controllers offer multiple set point configurations and also generates the independent multiple alarms.
Some of these standalone controllers include Yokogava temperature controllers, Honeywell PID controllers, OMEGA auto tune PID controllers, ABB PID controllers and Siemens PID controllers.
Most of the control applications, PLCs are used as PID controllers. PID blocks are inbuilt in PLCs/PACs and which offers advanced options for a precise control. PLCs are more intelligent and powerful than standalone controllers and make the job easier. Every PLC consist the PID block in their programming software, whether it can Siemens, ABB, AB, Delta, Emersion, or Yokogava PLC.
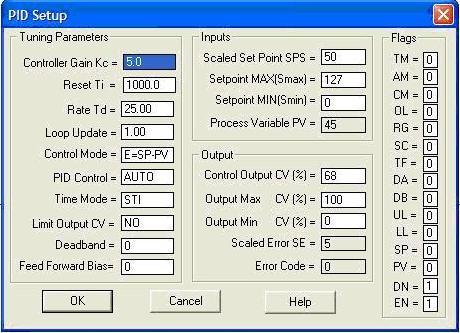
The figure below shows the Allen Bradley (AB) PID block and its setup window.
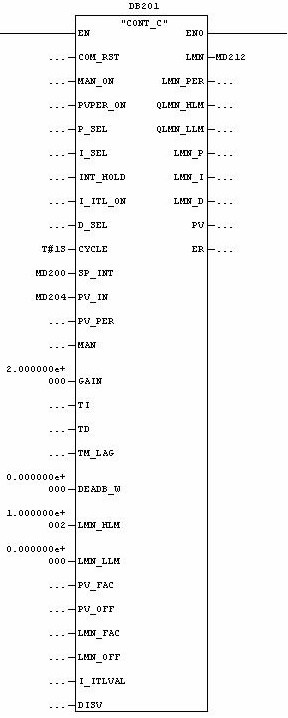
The figure below shows the Siemens PID block.
The below figure shows PID controller VIs offered by LabVIEW PID toolset.
FAQs
- What is a PID Controller?
- A PID controller is a feedback control system that utilizes three components: Proportional (P), Integral (I), and Derivative (D) actions to regulate a process variable and maintain it at a desired setpoint.
- What does PID stand for?
- PID stands for Proportional-Integral-Derivative, representing the three components that make up the controller.
- How does a PID Controller work?
- The controller continuously calculates an error signal, which is the difference between the desired setpoint and the actual process variable. The P, I, and D components are then applied to adjust the control output.
- Where are PID Controllers used?
- PID controllers find widespread use in industrial automation and process control systems. They are employed in applications such as temperature control, pressure regulation, speed control, and more.
- What is the role of Proportional (P) action in a PID Controller?
- The Proportional action responds to the current error, adjusting the control output in proportion to the magnitude of the error.
- What does Integral (I) action do in a PID Controller?
- The Integral action addresses accumulated errors over time, helping eliminate any steady-state errors that may persist with proportional control alone.
- How does Derivative (D) action contribute to PID control?
- The Derivative action considers the rate of change of the error, predicting future errors and contributing to system stability.
- What is the importance of tuning PID coefficients?
- Tuning PID coefficients (P, I, D) is crucial for optimizing the controller’s performance in a specific application, ensuring a balance between responsiveness and stability.
- Can PID Controllers be used in non-industrial settings?
- Yes, PID controllers are versatile and can be applied in various non-industrial settings, including robotics, home automation, and other control systems.
-
How do you tune a PID Controller?
- PID tuning involves adjusting the proportional, integral, and derivative coefficients to achieve the desired system response. This process often requires experimentation and fine-tuning based on the characteristics of the controlled system.
Related Posts:
- Design & Installation of Control & Monitoring Systems in Electrical Engineering
- What are Industrial Communication Networks? An Overview
- Metering, Energy Metering, Monitoring & Measurement Transducers
- Failures In Electrical Systems, Equipment & Materials
- What Exactly Is A Smart Grid? Smart Grid Applications
- Integration of Renewable Energy with Grid System
- What is Soft Starter? Its Working, Diagram and Applications
- Star Delta Starter – (Y-Δ) Starter Power, Control and Wiring Connection
- STAR-DELTA Starter Motor Starting Method Without Timer
- Direct Online Starter – DOL Starter Wiring Diagram for Motors
- What is Motor Starter? Types of Motor Starters and Motor Starting Methods
- Motor Protection – Types of Faults and Protection Devices
- Types of Electric Motors – Classification of AC, DC & Special Motors
- What is a Contactor ? Types, Working and Applications
- Why Do We Need to Install a Starter with a Motor?
- Single-Phase Induction Motor – Construction, Working, Types & Applications
- Three-Phase Induction Motor – Construction, Working, Types & Applications
- What Exactly Is A Smart Grid? Smart Grid Applications
- Integration of Renewable Energy with Grid System




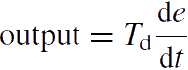








am asking about Automation system
You can read about Automation here.
Hello, please place dates and publishers please, hard to reference.
A team of professional engineers regularly updates the content to reflect the latest research. You can reference Electrical Technology for further information, with a link to the original article.
Realy I got what I was wondering.