Star to Delta & Delta to Star Conversion. Y-Δ Transformation
Star to Delta and Delta to Star Transformation – Y-Δ Conversion
In an electrical network, the impedance can be connected in various configurations. The most common of these configurations are either star or delta connected network. To solve complex electrical networks or simplify it, we use the star-delta conversion technique. It replaces any star connected network with its equivalent delta connected network & vice versa. We are going to provide a brief formula derivation for load conversion between star and delta connected load.
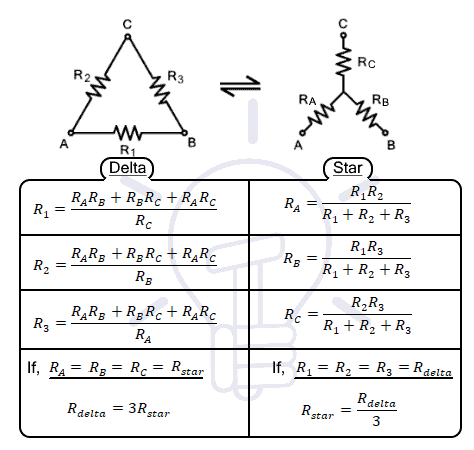
Star Delta Conversion
We know the basic of series, parallel or combo of series and parallel connection but Y-Δ is another little bit complex configuration of components. The 3-phase networks have three wires and usually, the networks are connected in star & delta configuration. The 3 phase supply or the load connected in either formation can be converted into its equivalent counterpart. We use such conversion to simplify the mathematical calculations required for circuit analysis of a complex electrical network.
Delta Connected Network
The delta connected network is formed when three network branches or impedances are connected to form a loop in such a way that their heads are connected to the tails of the adjacent branch. The resultant network forms a triangle shape that resembles a Greek letter Delta “Δ” which is why it’s named after it. It is also known as π (pi) network because it resembles the letter after rearranging the branches. Know more about Delta Connection in the previous post.
Star Connected Network
The Star connected network is formed when three branches or impedances are connected together at a common point. The other ends of the branch networks are free. The resultant shape resembles the letter “Y” which is why it is also called “Y” or “Wye” connected network. It is also known as “T” connected network due to its shape after rearranging the network branches. Know more about Star Connection in the previous post.
Delta to Star Conversion
The delta connected network can be transformed into star configuration using a set of electrical formula. Let’s derive the equation for each impedance.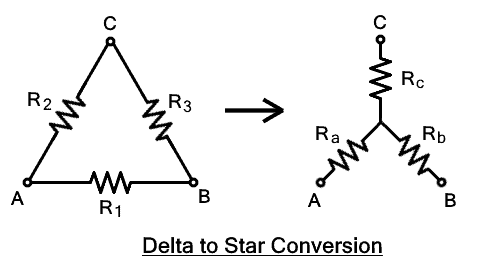
As mentioned earlier, the terminals A, B, C remains the same, as well as the impedance between them, must remain the same.
The total impedance between A-B in the delta network;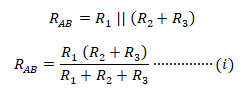


RAB = RA + RB
RBC = RB + RC
RAC = RA + RC
Now adding equation (i), (ii) & (iii) together
First, Subtract (ii) from (iv)
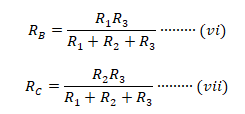
In case all three Impedances are same in a delta network, the equivalent star impedance would become

Star to Delta Conversion
Now we are going to convert the star connected impedance into delta connected impedance. Let’s derive the equations used for a star to delta conversion.

In order to find the equivalent delta resistance, multiply the previous equation (v) & (vi), as well as (vi) & (vii) & (v) & (vii) together.
Multiplying (v) & (vi)
Now add equation (viii), (ix) & (x) together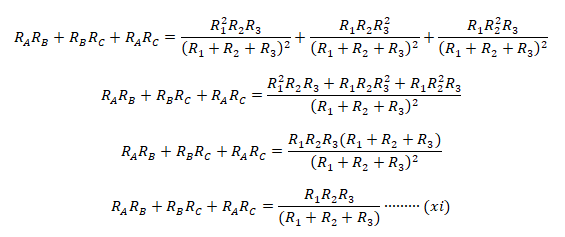
Dividing (xi) with (v)

Simplifying the equations will lead to
Using the previous equation,
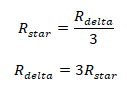
Related Posts:
- Thevenin’s Theorem. Step by Step Procedure with Solved Example
- Norton’s Theorem. Step by Step Procedure with Example
- SUPERNODE Circuit Analysis | Step by Step with Solved Example
- SUPERMESH Circuit Analysis | Step by Step with Solved Example
- Maximum Power Transfer Theorem for AC & DC Circuits
- Kirchhoff’s Current & Voltage Law (KCL & KVL) | Solved Example
- Compensation Theorem – Proof, Explanation and Solved Examples
- Substitution Theorem – Step by Step Guide with Solved Example
- Millman’s Theorem – Analyzing AC & DC Circuits – Examples
- Superposition Theorem – Circuit Analysis with Solved Example
- Tellegen’s Theorem – Solved Examples & MATLAB Simulation
- Voltage Divider Rule (VDR) – Solved Examples for R, L and C Circuits
- Current Divider Rule (CDR) – Solved Examples for AC and DC Circuits
- Ohm’s Law: Simple Explanation with Statement and Formulas
- Open Delta Connections of Transformers
- Star Delta Starter (Y-Δ) Starter – Power, Control & Wiring Diagram










I needed more of this. Thanks
I want to be a partaker of this learning