Home > Electrical Machines > Motors > Equivalent Circuit of Induction Motor

Equivalent Circuit of Induction Motor

0 5 minutes read

What is the Equivalent Circuit of Induction Motor?

An induction motor works on the principle of electromagnetic induction. The working of an induction motor is similar to the transformer. Also, an equivalent circuit of an induction motor is similar to the equivalent circuit of a transformer. The energy transfers in an induction motor from stator to rotor is a quite similar operation as energy transfers in the transformer from primary to secondary.

The induction motor is an asynchronous motor. And the speed of a motor depends on the loading condition. With the help of an equivalent circuit, we can evaluate the steady-state operation of the motor by simple network calculation and it enables us to find the performance characteristics like rotor torque, losses, and efficiency of the motor.

The induction motor always run below synchronous speed. The relative speed between the synchronous speed and actual rotor speed is known as slip. The equation of slip and synchronous speed is shown in the below equation.

Where,

N_s = Synchronous speed
N = Speed of rotor (actual speed)

Where,

f = Supply frequency
p = Number of poles

The equivalent circuit of an induction motor is drawn only for one phase.

Table of Contents

Stator Circuit Model

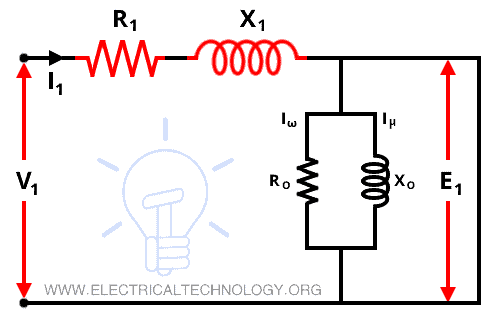
The stator model of an induction motor is shown in the figure below.

The stator consists of the stator winding and stator core. The loss produced in the stator winding is represented by the stator resistance R₁ and the loss produced in the stator core is represented by the stator reactance X₁. Therefore, the stator circuit model consists of a stator resistance and stator reactance connected in series.

The no-load current I₀ is divided into two parts; magnetizing current I_μ and core-loss current I_ω.

I₀ = I_μ + I_ω

A pure inductive reactance X₀ carries magnetizing current I_μ and non-inductive resistance carries core-loss current I_ω.

Due to the higher reluctance caused by the air gap in the case of the induction motor, the total magnetizing current is larger compared to the transformer. In an induction motor, the no-load current is 25 to 40% of the rated current and in a transformer, the no-load current is 2 to 5% of the rated current. The no-load current varies for different sizes and types of motors.

Rotor Circuit Model

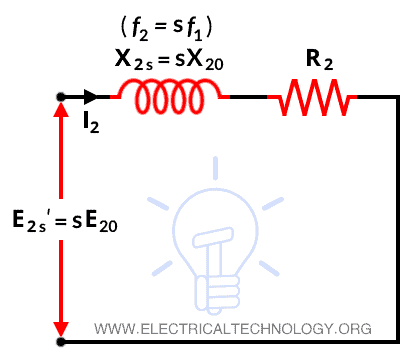
When a three-phase supply is given to the stator winding, the EMF is induced in the rotor winding. The rotor voltage depends on the relative motion of the rotor and stator magnetic field. The largest relative motion is achieved at standstill condition. The rotor voltage induced at any slip is given by;

E_2s = sE₂₀

If we ignore the skin effect, the rotor resistance is constant and it is independent of the slip. The rotor reactance depends on the rotor frequency and inductance. The rotor reactance is given by;

X₂ = 2πf₂ L₂

Where;

f₂ = rotor frequency
L₂ = rotor inductance

The relation between supply frequency f₁ and rotor frequency f₂ is given by;

f₂ = sf₁

X₂ = 2 πsf₁ L₂

X₂ = sX₂₀

Where;

X₂₀ = standstill reactance of rotor

The circuit diagram of the rotor circuit model is shown in the figure below.

From the above figure, the rotor impedance is given by;

Z_2s = R₂ + jX_2s

Z_2s = R₂ + jsX₂₀

The rotor current is given by;

Related Post:

This equation represents by the above figure-2. From this equation, it is noted that I₂s is a slip-frequency current produced by slip-frequency voltage sE₂₀ and rotor circuit having an impedance of R₂ + jX_2s.

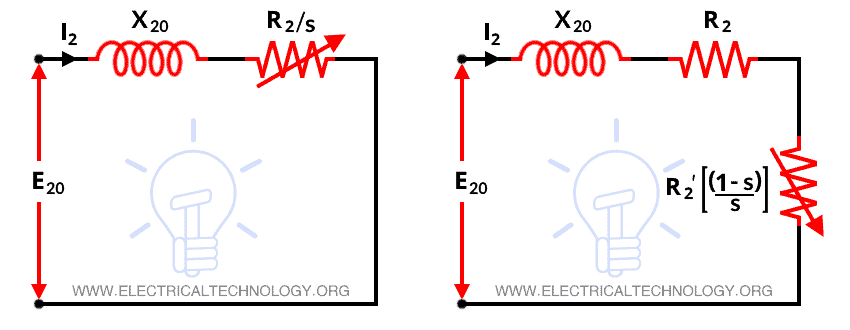
If we divide the above equation by slip s, we get;

The representation of this equation is shown in the figure below.

Here, we can see that the magnitude and phase angle of I₂s remains unchanged by this modification. Then also there is a huge difference between both equations. In equation-2, I₂s is produced by constant line frequency voltage E₂₀ and the rotor circuit has an impedance of (R₂/s) + jX₂₀. Therefore, I₂s in equation-2 is a line frequency current and I₂s in equation-1 is a slip-frequency current.

Also, in fig-2, the rotor circuit model has a constant resistance R₂ and variable leakage reactance sX₂₀. And in fig-3, the rotor circuit model has a constant leakage reactance X₂₀ and variable resistance R₂/s.

This equation describes similarity with the secondary winding of transformer having a constant voltage ratio and same frequency of both sides. Here, we assume a stationary rotor that carries the same current as the actual rotating rotor and produces the same MMF. This imaginary stationary rotor makes it possible to transfer secondary (rotor) impedance to the primary (stator) side.

In the case of induction motor, when the rotor current and voltages are referred to stator side, their frequency is also changed to stator frequency.

Exact Equivalent Circuit of Induction Motor

To derive the exact per-phase equivalent circuit of an induction motor, we need to calculate the rotor part of a model over to the stator circuit’s frequency and voltage level. In the transformer equivalent circuit, the voltage, current, and impedance on the secondary side are transferred to the primary side with the help of the turns ratio (a).

A similar transformation can be done in the case of the induction motor.

E₂‘ = a E₂ = E₁

R₂‘ = a²R₂

X₂₀‘ = a²X₂₀

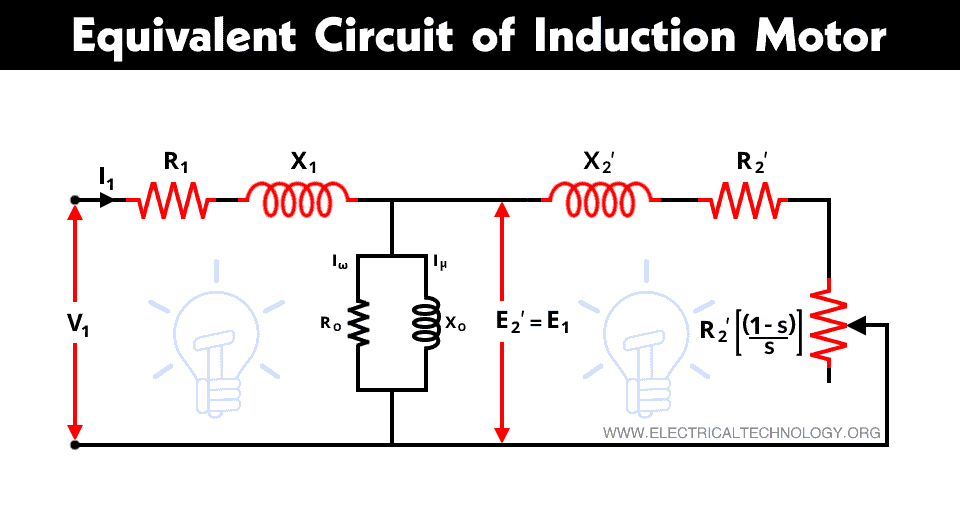
The exact equivalent circuit of the induction motor is shown in the figure below.

This equivalent circuit is identical to the two-winding transformer.

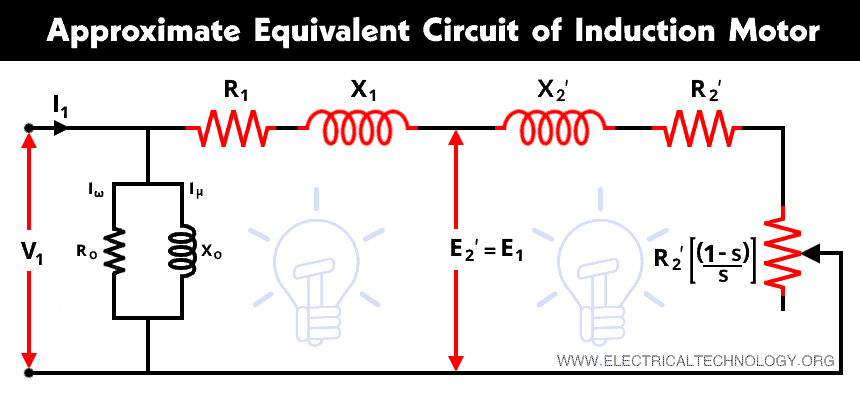
Approximate Equivalent Circuit of Motor

Like a transformer, in this case, also we can derive an approximate equivalent circuit by shifting the shunt impedance branches R₀ and X₀ to the input terminals. In an approximate equivalent circuit, we need to assume that;

V₁ ≈ E₁ = E₂‘

The approximate equivalent circuit of the induction motor is shown in the figure below.

As shown in the above figure, one resistance depends on the slip s. This resister represents the developed mechanical power by the rotor. All other components are constant. Reactances shown in the figure correspond to the fixed stator frequency f₁.

Equivalent Circuit of Induction Motor